C语言
C++
Python
C的目录
0.各种基础知识
1.排序算法
2.字符串操作
3.各种数据结构
3.1 链表
3.2 栈与队列
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
C++
Python
C的目录
0.各种基础知识
1.排序算法
2.字符串操作
3.各种数据结构
3.1 链表
3.2 栈与队列
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
C的目录
0.各种基础知识
1.排序算法
2.字符串操作
3.各种数据结构
3.1 链表
3.2 栈与队列
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
2.字符串操作
3.各种数据结构
3.1 链表
3.2 栈与队列
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
3.1 链表
3.2 栈与队列
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
3.3 树
3.4 哈希
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};
调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int * const ptr1 = months;
const int * ptr2 = months;
const int * const ptr3 = months;
以上代码中,ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。
管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。
外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改
内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。
- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long)
指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:
zippo == &zippo[0] == zippo[0] == &zippo[0][0]
- 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组
int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;
3.5 堆
0 各种基础知识
数组和指向数组的指针在大部分情况下都可以等同,但是只有指针表示法才可以进行自加/自减操作。
数组表示法:int arr[] = {1,2,3,4,5};
指针表示法:int *ptr = {1,2,3,4,5};调用其他函数对值进行修改,如果该函数无返回值,就需要将变量的地址作为实参传给目标函数,方能对该变量进行修改。
const: 如果函数的形参被const所修饰,则该函数无法修改该变量。
- 指向const的指针不能用于改变值。
- 可以把const数据或非const数据的地址传给const指针;但不能把const数据的地址传给普通指针,否则就可以通过指针修改这些数据了。
- 被const修饰的指针不能修改其指向的数据,但如果该数据自身不被const修饰,则可以通过其变量名进行修改。
const在指针类型前表示不能通过该指针进行其所指向的数据的修改操作;而const在指针类型后表示该指针不能指向别处(看与的相对位置,在左则不可修改指向的数值,在右则不可修改指向的地址),注意以下区别:
int* months = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; int * const ptr1 = months; const int * ptr2 = months; const int * const ptr3 = months;以上代码中,
ptr1不能被修改,即指向别的地址;ptr2则是不能直接修改months中的数值;ptr3则既不能更改其指向的地址,也不能修改其指向的地址上的值。
被static修饰的变量,在程序结束前都不会被销毁,但如果是在函数内声明该变量,则只能在该函数中使用。离开该函数后,变量的值会被保存下来,重新调用该函数时,不会进行初始化,而是沿用上一次调用后的数值。函数的声明中,形参不允许被static修饰。
限制作用域
用static修饰的函数,只能被在定义了该函数的模块中的函数调用,模块外的函数无法调用该函数,换句话说,如果在a.c文件中定义了函数static void func(),那么只有同在a.c文件中定义的函数才可以调用func(),而b.c文件中的函数只能通过a.c中的函数来调用func. 类似的,如果在一个文件中定义了一个全局变量,而该变量被static修饰,那么该变量就只能被该文件的函数使用,外部函数无法使用该变量。管理声明周期
函数中某个变量用static修饰,则函数返回后该变量的值被保留下来,下次调用该函数时沿用上一次调用时的变量值。
被
external修饰的变量可以被其他文件的函数所使用,使用前需要在所要使用该变量的其他源代码文件中使用extern关键字声明该变量。在同一文件中,如果某个函数内声明了与外部变量(或者叫全局变量)同名的变量且无额外的extern修饰(或被auto显式修饰,如果无其他关键字默认未auto),则全局变量在该函数中不可见;如果未进行声明或者声明时用extern进行修饰则可见。外部变量只能初始化一次。
const(constancy)对应恒常性,volatile(volatility)对应易变性。
const修饰的变量可初始化不可更改内存泄漏(memory leak)
静态内存的数量编译时就已经固定不变,而自动变量的内存数量在程序执行期间自动增加或减少,但是动态分配的内存数量只会增加。
但调用某个函数时,函数内使用malloc申请了一定的动态内存空间,如果返回时没有采用free()进行释放,则重新调用该函数时需要重新申请内存,原有内存块由于变量被销毁不能再重复访问,这就会导致内存被耗尽,这种现象被称为内存泄露。- calloc 申请的空间会初始化为0.
calloc(ElemType nitems, ElemType size); //nitems为元素个数,size为元素大小,如sizeof(long) 指针与多维数组
- 假设有如下声明:
int zippo[4][2];
则有如下关系:zippo == &zippo[0] == zippo[0] == &zippo[0][0] - 指向多维数组的指针:
int (* pz)[2]; //pz指向一个内含两个int类型的数组 int * px[2]; //px是一个内含两个指针元素的数组,每个元素都是指向int的指针- 假设有如下声明:
#define只是简单的进行替换,而typedef则是取别名.
#define STRING char *
STRING name, age;
char *name, age;
typedef char * STRING;
STRING name, age;
char *name, *age;上述代码中,第3行代码与第4行代码作用一致,而第7行则与第8行一致。(注意区别,前者只有name为指针,后者两个变量都是指针。)
- 函数指针
void ToUpper(char*); //函数原型
void (*pf)(char*); //pf是一个指向函数的指针
pf = ToUpper;声明时需要参数类型对应。
八进制以数字0开头,十六进制以0X或0x开头.
枚举
enum: 可以看作批量的define操作
1 排序算法
1.1 快排(quickSort)
ElemType FunctionName(){
//user code here
qsort(ElemType *arrName, ElemType arrSize, sizeof(ElemType),compare);
//user code here
}- 一维数组
ElemType cmp1(const void *a, const void *b){
return (*(ElemType *)a - *(ElemType *)b); //从大到小排序
//return *(ElemType *)a > *(ElemType *b);
}- 二维数组按某一列排序
ElemType cmp2(const void *a, const void *b){
return ((*(ElemType **)a)[i] - (*(ElemType **)b)[i]); //对矩阵按第i列从大到小排序
} 1.2 冒泡排序(bubbleSort)
基础版
冒泡排序是通过比较相邻两个位置的数的大小关系,如果后一个数小于前一个数,则将二者进行
swap,直至遍历完成整个数组。实现方法也比较简单,直接两个for循环遍历数组,两两比较相邻元素即可。因此,冒泡排序基础版的时间复杂度为$O(n^2)$,而空间复杂度则为$O(1)$.void bubbleSort(int *nums,int numsSize){ if(numsSize < 2) return; for(int i = 0; i < numsSize-1; i++){ for(int j = 1; j < numsSize-i; j++){ if(nums[j-1] > nums[j]){ swap(&nums[j-1], &nums[j]); } } } }
优化版
提前结束
基础版的冒泡排序需要遍历到数组的最后一个位置,但可能出现遍历到某个位置就已经完成排序,即完成某次内循环后再进行下一层内循环将不再进行swap操作,因而可以利用这个思路进行优化。void bubbleSort(int *nums,int numsSize){ if(numsSize < 2) return; for(int i = 0; i < numsSize-1; i++){ bool flag = false; for(int j = 1; j < numsSize-i; j++){ if(nums[j-1] > nums[j]){ swap(&nums[j-1], &nums[j]); flag = true; } } if(flag) break; } }提前结束+边界优化
除了上述的提前结束的思路之外,我们可以对记录前边作swap操作的最后位置,该位置之后的元素都已经是排好序了的,下一次内循环只需要遍历到该位置即可。void bubbleSort(int *nums,int numsSize){ if(numsSize < 2) return; bool flag = true; int last = numsSize - 1; int index = -1; while(flag){ flag = false; for(int i = 0; i < last; ++i){ if(nums[i] > nums[i+1]){ swap(&nums[i], &nums[i+1]); flag = true; index = i; } } last = index; } }
1.3 归并排序(mergeSort)
void mergeSort(int *nums,int left,int right){
if(left>=right) return;
int mid = left+(right-left)/2;
mergeSort(nums,left,mid);
mergeSort(nums,mid+1,right);
int tmp[right-left+1];
//divide
for(int k=left;k<=right;k++){
tmp[k-left] = nums[k];
}
//conquer
int i = 0,j = mid + 1 - left;
for(int k=left;k<=right;k++){
if(i==mid+1-left){
nums[k] = tmp[j++];
}else if(j==right-left||tmp[i]<=tmp[j]){
nums[k] = tmp[i++];
}else{
nums[k] = tmp[j++];
}
}
} 1.4 选择排序(SelectionSort)
基础版
选择排序其实就是两个
for循环进行数组遍历,内循环寻找外循环当前位置右边的最小值的索引,当内循环完成遍历后将最小值与外循环当前元素进行swap即可。int selecitonSort(int *nums,int numsSize){ if(numsSize < 2) return; for(int i = 0; i < numsSize-1; ++i){ int minIndex = i; for(int j = i+1; j < numsSize; ++j){ if(nums[j] < nums[minIndex]){ minIndex = j; } } swap(&nums[i], &nums[minIndex]); } }
优化版
上述的基础版选择排序为单元选择,即一次遍历只找当前位置右边的最小值并进行
swap,其实可以在遍历时顺带查找最大值,实现双元选择,但实际上这种方式对于性能的优化有限。int selecitonSort(int *nums,int numsSize){ if(numsSize < 2) return; for(int i = 0; i < numsSize-1-i; ++i){ int minIdx = i, maxIdx = i; for(int j = i+1; j < numsSize; ++j){ if(nums[j] < nums[minIdx]){ minIdx = j; }else if(nums[j] > nums[maxIdx]){ maxIdx = j; } } // 说明当前位置及右边的元素均相等 if(minIdx == maxIdx) break; // 若本轮第一个数字不是最小值,则交换位置(将最小值与本轮第一个数字交换位置) if(minIdx != i) swap(&nums[i], &nums[minIdx]); // 在交换i和minIdx时,有可能出现i即maxIdx的情况,此时需要修改maxIdx为minIdx if(maxIdx == i) maxIdx = minIdx; // 若本轮最后一个数字不是最大值,则交换位置(将最大值与本轮最后一个数字交换位置) if(maxIdx != numsSize-1-i) swap(&nums[maxIdx], &nums[numsSize-1-i]); } }
1.5 插入排序(Insert Sort)
基础版
插入排序是选定当前遍历的位置的元素(插入元素),然后遍历其左边的元素(比较元素),当比较元素大于插入元素时,则继续向左边寻找插入位置直至找到比较元素小于等于插入元素,此时将插入元素插入当前位置即可。
void insertSort(int* nums, int numsSize){ if(numsSize < 2) return; for(int i = 1; i < numsSize; ++i){ int j = i-1, tmp = nums[i]; for(; j >= 0; --j){ if(nums[j] > nums[i]){ nums[j+1] = nums[j]; }else{ break; } } if(j != i-1){ nums[j+1] = tmp; } } }
优化版
基础版需要逐位查找相应的插入位置,但实际上当前位置左侧的子数组已经是排过序了的,因此可以借用二分查找的思路来查找插入位置。
void insertSort(int* nums, int numsSize){ if(numsSize < 2) return; for(int i = 1; i < numsSize; ++i){ if(nums[i-1] < nums[i]) continue; int l = 0, r = i - 1, tmp = nums[i]; while(l <= r){ int m = l + (r - l)/2; if(nums[m] > nums[i]){ r = m - 1; }else{ l = m + 1; } } for(int j = i; j > l; --j){ //移动 nums[j] = nums[j-1]; } nums[l] = tmp; // 插入 } }
1.6 计数排序(Counting Sort)
- 计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
- 具体做法是:①找出待排序中最大元素,记为MAX;②申请长度为(MAX+1)的数组,遍历数组并对每个元素的次数进行统计;③对所有的计数进行累加;④反向填充数组。
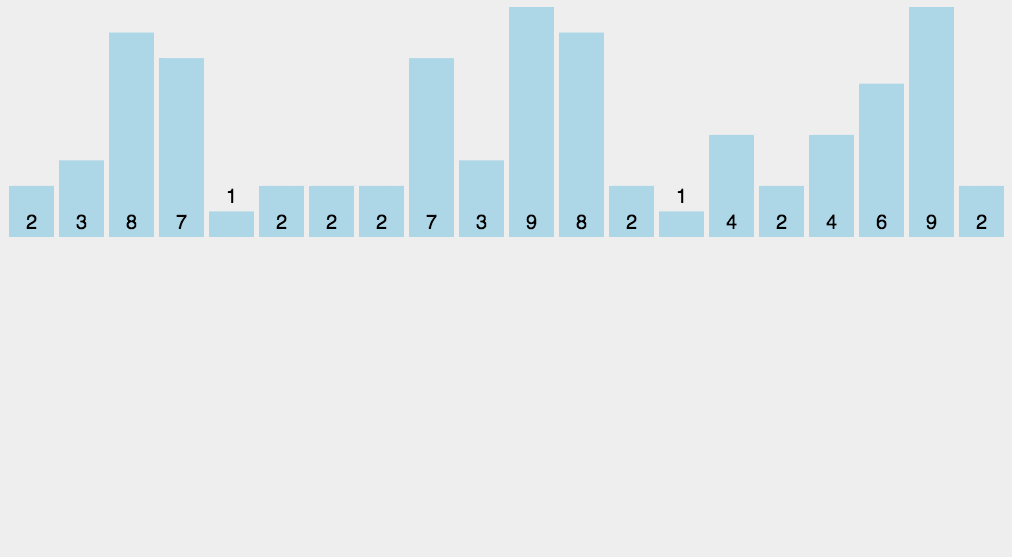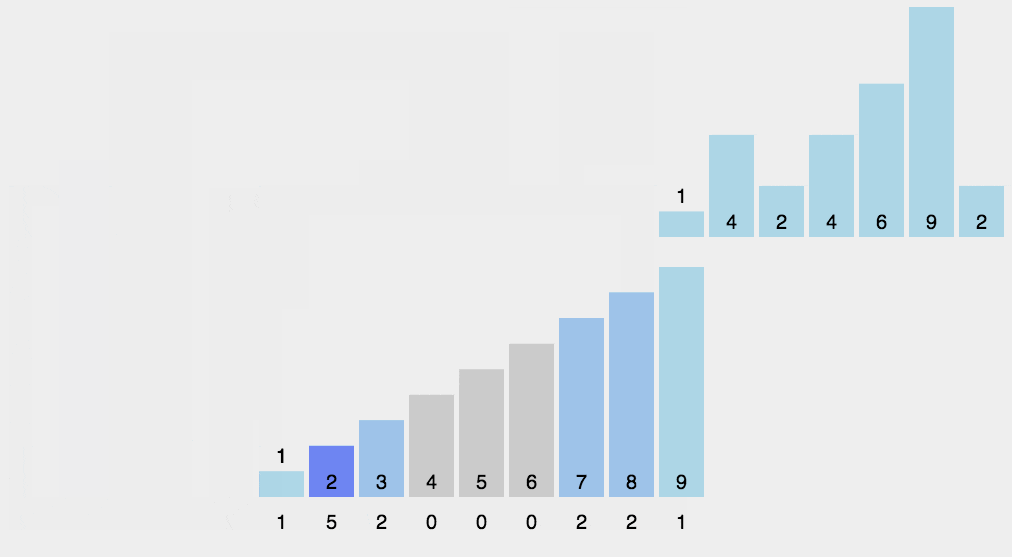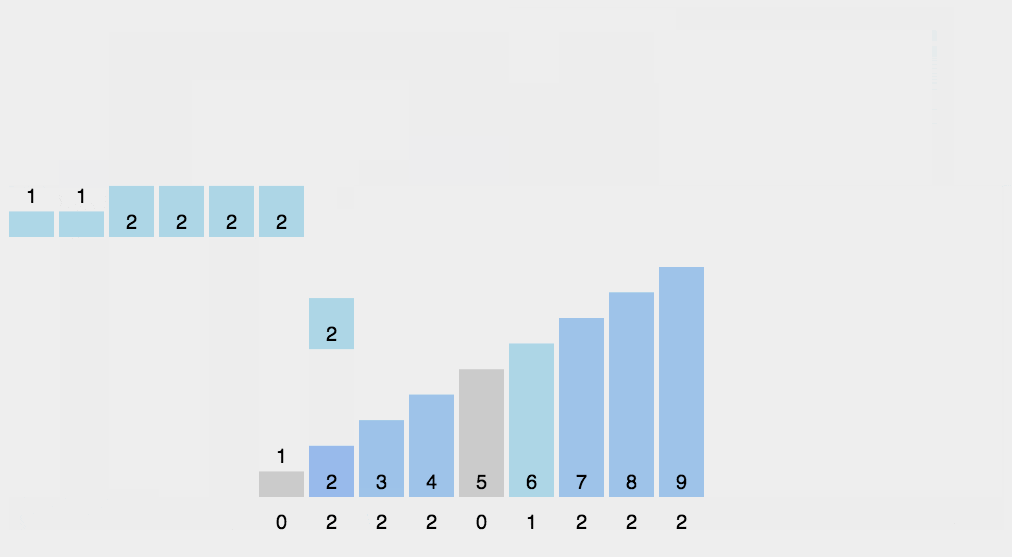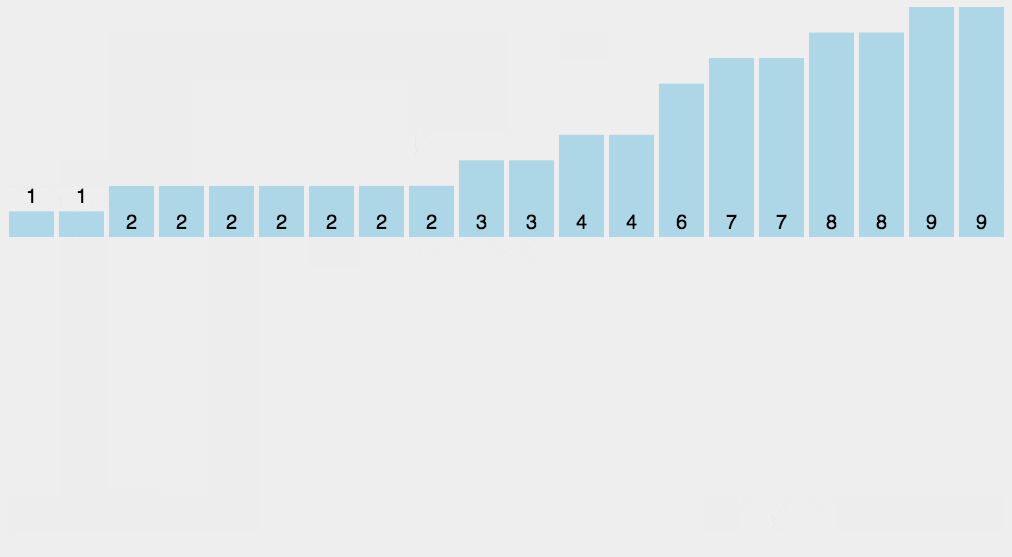
/*************************************************************************************
* 缺 点:浪费空间,即使记录min,然后tmp长度设为(max-min)+1,某些情况下还是存在空间浪费
*
* 因此,运用计数排序的前提是待排序数组的取值在一定范围内且较为集中
**************************************************************************************/
#include <math.h>
void findMaxMinVal(int *max, int *min, int *nums, int numsSize){
for(int i = 0; i < numsSize; i++){
*max = fmax(*max, nums[i]);
*min = fmin(*min, nums[i]);
}
}
int *countingSort(int *nums, int numsSize){
int max = INT_MIN, min = INT_MAX;
findMaxMinVal(&max, &min, nums, numsSize);
int size = max - min + 1;
int tmp[size] = {0};
int *ret = (int *)malloc(sizeof(int)*numsSize);
for(int i = 0; i < numsSize; i++){ //进行计数
tmp[nums[i]-min] += 1;
}
for(int i = 1; i < size; i++){
tmp[i] += tmp[i-1];
}
for(int i = numsSize; i >0; i--){
ret[--tmp[nums[i-1]]] = nums[i];
}
free(tmp);
return ret;
} 1.7 桶排序(Bucket Sort)
桶排序是计数排序的扩展。利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
①在额外空间充足的情况下,尽量增大桶的数量;
②使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中。
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。(分完桶要对每个桶内元素进行排序)
1.8 基数排序(Radix Sort)
基数排序是桶排序的扩展。
原理:将整数按位数切割成不同的数字,然后按每个位数分别比较。
具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

/********************************************************************
* 输 入 : nums为待排序的数组, numsSize为数组大小, exp为指数
* 当exp=1时对个位数进行排序,为10则对十位数进行排序......
*********************************************************************/
void countSort(int *nums, int numsSize, int exp){
int bucket[10] = {0}, tmp[numsSize];
for(int i = 0; i < numsSize; i++){ //将数组元素按当前排序位放入对应的桶中
bucket[(nums[i]/exp)%10] += 1;
}
for(int i = 1; i < 10; i++){
bucket[i] += bucket[i-1]; //将桶中元素个数作前缀和,以便后续按顺序输出
}
for(int i = numbersSize - 1; i >= 0; i--){
tmp[bucket[(nums[i]/exp)%10] - 1] = nums[i]; //将桶中元素按顺序拿出并放入临时数组tmp中
bucket[(nums[i]/exp)%10] -= 1;
}
for(int i = 0; i < numbersSize; i++){
nums[i] = tmp[i]; //将排序后的tmp数组返回给nums
}
}
int* radixSort(int *nums, int numsSize){
int max = nums[0];
for(int i = 1; i < numsSize; i++){ //找到数组中的最大值,用来确定需要进行多少位(次)排序
max = fmax(max, nums[i]);
}
for(int exp = 1; exp < max; exp *= 10){ //按个、十、百、千...的顺序逐步进行排序
countSort(nums, numsSize, exp);
}
return nums;
} 1.9 堆排序(Heap Sort)
- 构建大顶堆:

- 下滤:
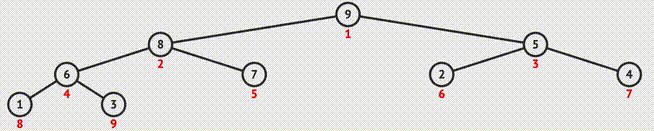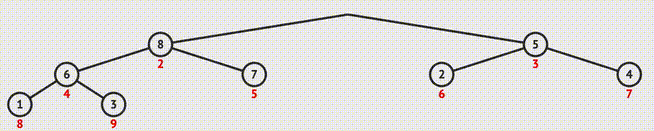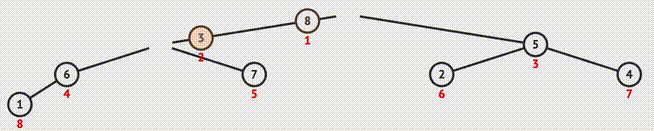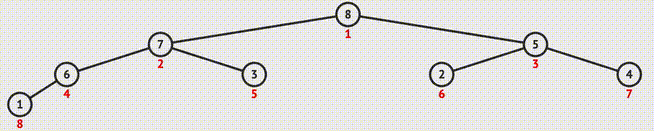
迭代实现
// 下滤操作 void siftDown(int* nums, int curIdx, int endIdx){ int tmp = nums[curIdx]; int childIdx = curIdx * 2 + 1; while(childIdx <= endIdx){ if(childIdx < endIdx && nums[childIdx+1] > nums[childIdx]){ ++childIdx; } if(nums[childIdx] > tmp){ nums[curIdx] = nums[childIdx]; curIdx = childIdx; childIdx = curIdx * 2 + 1; }else{ break; } } nums[curIdx] = tmp; } // 构建大顶堆 void heapify(int* nums, int endIdx){ for(int i = (endIdx - 1)/2; i >= 0; --i){ siftDown(nums, i, endIdx); } } // 堆排序(原地) void heapSort(int* nums, int numsSize){ if(numsSize < 2) return; heapify(nums, numsSize - 1); for(int i = numsSize - 1; i >= 0; --i){ swap(&nums[0], &nums[i]); siftDown(nums, 0, i-1); } }递归实现
// 交换
void swap(int *num1, int *num2){
int tmp = *num1;
*num1 = *num2;
*num2 = tmp;
}
// 维持堆性质
void heapify(int *arr, int arrSize, int index){
int largest = index;
int lson = 2 * index + 1;
int rson = 2 * index + 2;
if(lson < arrSize && arr[lson] > arr[largest]){
largest = lson;
}
if(rson < arrSize && arr[rson] > arr[largest]){
largest = rson;
}
if(index != largest){
swap(&arr[largest], &arr[index]);
heapify(arr, arrSize, largest); // 递归建堆大顶
}
}
// 堆排序
void heapSort(int *arr, int arrSize){
for(int i = (arrSize-1)/2; i >= 0; --i){
heapify(arr, arrSize, i);
}
for(int i = arrSize - 1; i > 0; --i){
swap(&arr[0] &arr[i]);
heapify(arr, i);
}
} 2 字符串操作
用双引号括起来的是字符串字面量,也叫字符串常量;用单引号括起来的是字符常量。对于双引号中的字符,编译器会自动加入’\0’字符。
字符串常量之间若没有间隔或用空白字符分隔,则会被串联起来。
用双引号括起来的内容被视为指向该字符串存储位置的指针,类似数组的指针等同于数组中第一个元素的地址。考虑如下代码:
int main{
printf("%s, %p, %c\n", "We", "are", *"space farers");
return 0;
}其输出为:
We, 0x100000f61, s- 字符串数组的空间必须比字符串中的字符数多1.
2.1 字符串、字符串数组与字符数组的区别
- 字符数组: 数组存放的数据类型为字符,声明:
char *str = {'w','o', 'r', 'l', 'd'};. 对于字符数组,有:strlen(str) == sizeof(str)/sizeof(char) == 5.
- 字符串: C语言中,字符串用字符数组来表示,跟字符数组类似,不同的是最后是以’\0’空字符为结尾,而字符数组没有这个所谓的结尾. 声明:
char str* = "world;". 此时有:strlen(str) == 5,而sizeof(str) == 6.(strlen()不将字符串中的\0计算到串的长度,而sizeof()会)
- 字符串数组:数组中存放的数据类型为字符串,相当于二维的字符数组(但是每一行的最后一个都是
'\0').
2.2 常见字符处理函数
2.2.1 scanf()
函数功能:从键盘获得用户输入
- 对于
scanf(),输入数据的格式要和控制字符串的格式保持一致. 与printf类似,都有变量列表,不同的是printf的变量列表都是变量名即可,而scanf需要在变量名前加上&来获取变量在内存中的地址 - 从键盘输入的数据并没有直接交给
scanf(),而是放入了缓冲区中,直到我们按下回车键, scanf() 才到缓冲区中读取数据。如果缓冲区中的数据符合 scanf() 的要求,那么就读取结束;如果不符合要求,那么就继续等待用户输入,或者干脆读取失败。scanf() 不会跳过不符合要求的数据,遇到不符合要求的数据会读取失败,而不是再继续等待用户输入。
scanf()的格式控制符汇总如下表:
| 格式控制符| 说明 |
| ————-|———|
|%c|读取一个单一的字符|
|%hd、%d、%ld|读取一个十进制整数,并分别赋值给 short、int、long 类型|
|%ho、%o、%lo|读取一个八进制整数(可带前缀也可不带),并分别赋值给 short、int、long 类型|
|%hx、%x、%lx|读取一个十六进制整数(可带前缀也可不带),并分别赋值给 short、int、long 类型|
|%hu、%u、%lu|读取一个无符号整数,并分别赋值给 unsigned short、unsigned int、unsigned long 类型|
|%f、%lf|读取一个十进制形式的小数,并分别赋值给 float、double 类型|
|%e、%le|读取一个指数形式的小数,并分别赋值给 float、double 类型|
|%g、%lg|既可以读取一个十进制形式的小数,也可以读取一个指数形式的小数,并分别赋值给 float、double 类型|
|%s|读取一个字符串(以空白符为结束)|
2.2.2 getchar()
scanf("%c", c)的替代品,除了更加简洁,没有其它优势了; 或者说,getchar() 就是 scanf() 的一个简化版本.
下面的代码演示了 getchar() 的用法:
#include <stdio.h>
int main()
{
char c;
c = getchar();
printf("c: %c\n", c);
return 0;
}输入实例:
@↙
c: @2.2.2 getche()
没有缓冲区,输入一个字符后会立即读取,不用等待用户按下回车键,这是它和 scanf()、getchar() 的最大区别。请看下面的代码:
#include <stdio.h>
#include <conio.h>
int main()
{
char c = getche();
printf("c: %c\n", c);
return 0;
}输入示例:
@c: @输入@后,getche() 立即读取完毕,接着继续执行 printf() 将字符输出,所以没有按下回车键程序就运行结束了。
2.2.3 printf()
2.2.4 puts
- 与printf的区别:
puts()只显示字符串,并在字符串末尾加上换行符.
int main(){
char words[81] = "I am a string in an array.";
const char *ptr1 = "Something is pointing at me.";
puts("Here are some strings:");
puts(words);
puts(ptr1);
return 0;
}输出如下:
Here are some strings:
I am a string in an array.
Something is pointing at me. 3 各种数据结构
3.1 链表
3.1.1 简介
- 单链表:结点由一个数据域和指针域构成,其中指针域存储当前结点的后继元素的地址。
- 双链表:除了一个数据域、一个存放后继元素的指针域,还有一个指针域用于存放当前结点的前趋元素的地址。
循环链表:链表首尾相接。单链表中最后一个元素的指针域为空(NULL),而循环链表则指向第一个结点元素,即tail->next = head.
头指针:指向链表第一个结点的指针,其实就是*head
- 首元结点:存储第一个数据元素的结点
- 头结点:首元结点前的虚拟结点dummyHead
- dummyHead的作用:便于对首元结点的操作,如插入与删除,并且其处理与其他位置的处理时一致的,无需额外的特殊处理。其val可以存一些关键信息,如链表长度。
访问链表,只能通过头指针进入链表,结点需要按顺序访问。
3.1.2 结构体定义
typedef struct ListNode{
ElemType val; //数据域,存放data
struct ListNode *next; //指针域,指向当前节点的后继节点,存放地址
//struct ListNode *prev; //指针域,指向当前节点的前趋节点
}ListNode;其中,*next/*prev用struct ListNode定义,表示其指向的数据元素也是包括这两项的,也就是套娃
3.1.3 链表的基本操作
- 遍历查询
ElemType funcName(struct ListNode *head, ElemType param){
//...
struct ListNode *cur = head;
while(cur && (some condition needed to be handle)){
cur = cur->next;
//handle code here like save the val to an array or change the val
}
...
}- 插入节点
- 尾插法
struct ListNode insertNode(struct ListNode *obj, int val){
struct ListNode *cur = obj; //用于遍历链表的变量
struct ListNode *node = (struct ListNode *)malloc(sizeof(struct ListNode));
node->val = val;
node->next = NULL;
while(cur && cur->next){ //找到最后一个节点
cur = cur->next;
}
cur->next = node;
return obj;
}- 头插法
struct ListNode insertNode(struct ListNode *obj, int val){
struct ListNode *node = (struct ListNode *)malloc(sizeof(struct ListNode));
node->val = val;
node->next = next;
obj->next = node;
return obj;
}- 删除节点
- LeetCode 19. 删除链表的倒数第N个结点
问题描述:给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点.
思路:创建两个指针,初始化都头结点,fast指针先向后移动n个结点,然后fast和slow指针同时向后移动直至fast->next为空,说明此时slow->next即为倒数第N个结点,直接将slow->next指向下下个结点,即slow->next = slow->next->next.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeNthFromEnd(struct ListNode* head, int n){
struct ListNode* slow = head, *fast = head, *tmp;
for(int i = 0 ; i < n; i++){
if(!fast) return head;
fast = fast->next;
}
while(fast && fast->next){
fast = fast->next;
slow = slow->next;
}
tmp = slow->next;
slow->next = slow->next->next;
free(tmp);
return head;
}- LeetCode 82. 删除排序链表中的重复元素II
问题描述:给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表。
思路: 用prev存放更新后的链表中的最后一个非重复性结点,用cur指针遍历链表,当cur->val == cur->next->val时,说明当前结点为重复性结点,记录当前的val,当当前结点的val等于这个值时指针后移一位;当检测到非重复性结点时,将prev的next域指向该结点,并将prev和cur同时后移一位。由于原链表中的头结点可能为重复性结点,因此需要创建一个虚拟头结点dummyHead来统一处理。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* deleteDuplicates(struct ListNode* head){
if(!head) return head;
struct ListNode *dummyHead = malloc(sizeof(struct ListNode));
dummyHead->next = head;
struct ListNode *prev = dummyHead, *cur = head;
while(cur){
if(cur->next && cur->val == cur->next->val){
int delVal = cur->val;
while(cur && cur->val == delVal){
cur = cur->next;
}
prev->next = cur;
}else{
prev = prev->next;
cur = cur->next;
}
}
return dummyHead->next;
}翻转链表
LeetCode 206. 反转链表
- 递归
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* reverseList(struct ListNode* head){
if(!head || !head->next) return head;
struct ListNode *newHead = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return newHead;
}- 迭代(双指针)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* reverseList(struct ListNode* head){
if(!head || !head->next) return head;
struct ListNode *prev = NULL, *cur = head;
while(cur){
struct ListNode *next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
return prev;
}检查是否成环
LeetCode 141. 环形链表
问题描述:给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
思路:快慢指针,如果快慢指针出现相等的情况说明有环,当快指针为NULL说明无环。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode *head) {
struct ListNode *fast = head, *slow = head;
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
if(fast == slow) return true;
}
return false;
} 3.2 栈与队列
3.3 树
3.3.1 简介
树是一种树状的数据结构,其节点间的关系如同大树一般,按照不同的层次关系形成了节点间的父子关系。按照子节点个数可以分为二叉树、三叉树、多叉树等,如果子节点个数为 1 其实就是链表。
树中除了根节点之外,其余节点均有父节点,而没有子节点的节点称为叶节点。
树其实可看作是链表的高配版。树的实现就是对链表的指针域进行了扩充,增加了多个地址指向子结点。同时将“链表”竖起来,从而凸显了结点之间的层次关系,更便于分析和理解。
前边提到的二叉树,按照节点间的大小关系和节点的数量还可以分为以下几种不同的树:
- 完全二叉树: 除了最后一层结点,其它层的结点数都达到了最大值;同时最后一层的结点都是按照从左到右依次排布。
- 满二叉树: 除了最后一层,其它层的结点都有两个子结点。
- 二叉排序树: 是一棵空树,或者若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉排序树。(按中序遍历后结果为有序数组)
- 平衡二叉树: 平衡二叉树又被称为AVL树,它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
- 红黑树: 红黑树通过将结点进行红黑着色,使得原本高度平衡的树结构被稍微打乱,平衡程度降低。红黑树不追求完全平衡,只要求达到部分平衡。这是一种折中的方案,大大提高了结点删除和插入的效率。
3.3.2 二叉树性质
二叉树第
i层上的节点树最多为$2^{i-1}$个。深度为
k的二叉树的节点总数量最多为$2^k - 1$(等比数列求和)。包含
n个节点的二叉树高度最少为log2(n)+1或者log2(n+1),最大高度为n。在任意一棵二叉树中,若叶节点的个数为$n_0$, 度为
2的节点数为$n_2$(即有两个子节点的节点),则有$n_0 = n_2 + 1$。
记度为
0(即叶节点)的数量为$n_0$、度为1的为$n_1$、度为2的为$n_2$, 则二叉树中的节点数量为$n = n_0 + n_1 + n_2$,而边数则应该满足$n - 1 = 2n_2 + n_1$即$n_0 + n_1 + n_2- 1 = 2n_2 + n_1$,合并得到$n_2 + 1 = n_0$
3.3.3 存储方式
链式存储,可分为双亲表示法、孩子表示法以及孩子兄弟表示法
顺序存储:用数组来存储二叉树,这种存储方式有一个特别好用的性质:如果父节点的数组下标为
i,则其左右孩子的下标分别为2i+1和2i+2(数组表示中NULL节点也要占一个位置)。
3.3.4 构造方式
- 结构体定义
typedef struct MyBinaryTree {
int val;
struct MyBinaryTree *lChild; //左孩子指针
struct MyBinaryTree *rChild; //右孩子指针
}BinaryTree;树的构造(以数组为例)
先通过数组创建二叉树结点数组
BinaryTree** nodes = (BinaryTree**)malloc(sizeof(BinaryTree*)*numsSize); for(int i = 0; i < numsSize; ++i){ if(nums[i] == -1){ nodes[i] = NULL; }else{ nodes[i] = (BinaryTree*)malloc(sizeof(BinaryTree)); nodes[i]->val = nums[i]; nodes[i]->lChild = NULL; nodes[i]->rChild = NULL; } }遍历二叉树结点数组,
i的left指向2i+1,i的right指向2i+2. 注意要判断2i+2是否越界。for(int i = 0; 2*i+2 < numsSize; ++i){ if(!nodes[i]){ continue; } nodes[i]->lChild = nodes[2*i+1]; nodes[i]->rChild = nodes[2*i+2]; }
3.3.5 二叉树的遍历
二叉树的遍历方式一般有4种:前序遍历、中序遍历、后序遍历以及层序遍历。前三种属于深度优先遍历(因而需要用到栈),后一种则是广度优先遍历(因而需要用到队列)。
- 前序遍历:从根节点开始遍历,按照根结点-左孩子-右孩子的顺序进行遍历.
- 中序遍历:按照左孩子-根结点-右孩子的顺序进行遍历.
- 后序遍历:按照左孩子-右孩子-根结点的顺序进行遍历.
- 层序遍历:按照层数进行遍历,一般是当前所在层按照由左而右的顺序进行遍历.
前序遍历的实现
顺序为根-左-右,因而遍历过程中直接把当前遍历到的结点的值插入到答案中,将当前结点入栈后优先访问左子树直至左子树为
NULL;将栈顶结点赋给遍历变量,然后对当前结点的右子树进行遍历。迭代实现
int* preOrderTraverse(BinaryTree* root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; BinaryTree* cur = root; while(cur || stk_top != 0){ while(cur){ stack[stk_top++] = cur; res[(*returnSize)++] = cur->val; cur = cur->lChild; } cur = stack[--stk_top]; cur = cur->rChild; } return res; }递归实现
void preOrderTraverse3(BinaryTree *root, int *res, int *returnSize){ if(!root) return; res[(*returnSize)++] = root->val; //先中 preOrderTraverse3(root->lChild, res, returnSize);//后左 preOrderTraverse3(root->rChild, res, returnSize);//再右 }
中序遍历的实现
顺序为左-根-右,需要先访问完当前结点的左子树再将当前结点的值加入到答案中,因而需要一直访问左子树直至左子树为
NULL,再把当前结点的值加入答案,然后访问右孩子。迭代实现
int* inOrderTraverse(BinaryTree* root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; BinaryTree* cur = root; while(cur || stk_top != 0){ while(cur){ stack[stk_top++] = cur; cur = cur->lChild; } cur = stack[--stk_top]; res[(*returnSize)++] = cur->val; cur = cur->rChild; } return res; }递归实现
void inOrderTraverse3(BinaryTree *root, int *res, int *returnSize){ if(!root) return; inOrderTraverse3(root->lChild, res, returnSize); //左 res[(*returnSize)++] = root->val; //中 inOrderTraverse3(root->rChild, res, returnSize); //右 }
后序遍历的实现
后序遍历的顺序为左-右-根,直接迭代似乎无法做到先访问完左右子树后再访问自己,但是可以发现后序遍历的顺序其实是
根-右-左的翻转后的顺序,因此,可以采用根-右-左的顺序进行遍历,这个顺序其实就类似前序遍历,只是这里先访问右孩子,而前序则是先访问左孩子。遍历完翻转一下结果就实现了后序遍历;或是通过递归来实现。迭代实现(+翻转)
void reverse(int **res, int l, int r){ //翻转 while(l < r){ int num = (*res)[l]; (*res)[l++] = (*res)[r]; (*res)[r--] = num; } } int* postOrderTraverse(BinaryTree* root, int *returnSize){ //根右左+翻转 if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; BinaryTree* cur = root; while(cur || stk_top != 0){ while(cur){ stack[stk_top++] = cur; res[(*returnSize)++] = cur->val; //先根 cur = cur->rChild; //后右 } cur = stack[--stk_top]; cur = cur->lChild; //再左 } reverse(&res, 0, *returnSize-1); //最后翻转一下 return res; }递归实现
void postOrderTraverse3(BinaryTree *root, int *res, int *returnSize){ if(!root) return; postOrderTraverse3(root->lChild, res, returnSize); //先左 postOrderTraverse3(root->rChild, res, returnSize); //后右 res[(*returnSize)++] = root->val; //再根 }
层序遍历的实现
层序遍历是按照每一层的顺序来进行遍历,因而我们需要借用队列这一数据结构,访问当前结点,然后把其左孩子和右孩子插入队列中,直到把这一层的结点访问完就进行下一层的访问。因而需要创建一个变量用来记录当前所在的层的结点数,结点数为队列尾指针减去头指针的差。要注意,获取当前层的结点数需要在访问该层结点的开始前进行,否则访问该层的时候由于会插入该节点的左孩子和右孩子,将会导致队列中结点数的改变。
实现代码如下。
//层序遍历 int* layerTraverse(BinaryTree* root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* queue[MAX_NODE_NUM]; //创建队列 int front = 0, rear = 0; //头指针、尾指针 *returnSize = 0; queue[rear++] = root; //将根节点插入队列中,此时为第一层 while(front != rear){ //当队列不为空说明遍历未完成 int size = rear - front; //获取当前队列中的结点数,其实就是当前层的节点数 while(size--){ //每次访问一个结点就将节点数减1 BinaryTree* cur = queue[front++]; res[(*returnSize)++] = cur->val; if(cur->lChild) queue[rear++] = cur->lChild; if(cur->rChild) queue[rear++] = cur->rChild; } } return res; }
统一迭代遍历
通过上边前序、中序、后序遍历的迭代实现可以发现,三者的代码并不统一,特别后序遍历还需要进行一次翻转操作。其实可以用一种更为清晰的思路来实现,三者仅需要调整三个入栈语句的顺序即可。
遍历过程中采用栈结构来存储尚且未遍历的结点,这样无法同时解决遍历到的结点和下一个待处理结点不一致的情况,如中序遍历中当前遍历到的结点为根节点,而我们先处理的应该是左结点。因此在结点入栈时我们需要对结点进行标记,通过在待处理结点入栈后压入一个空结点,那么以后从栈中弹出结点,如果弹出的结点为空结点,说明当前栈顶结点就是我们要处理的结点;否则,说明还没到处理的结点,将三个结点按顺序入栈。注意:由于栈是
FILO的结构,压入和弹出的顺序是相反的,因而我们在压栈的时候要反过来。
前序遍历先处理的是根节点,因而其入栈顺序为
右-左-根-NULL.实现代码如下:
int* preOrderTraverse2(BinaryTree *root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; stack[stk_top++] = root; while(stk_top != 0){ BinaryTree* cur = stack[--stk_top]; if(cur){ if(cur->rChild) stack[stk_top++] = cur->rChild; if(cur->lChild) stack[stk_top++] = cur->lChild; stack[stk_top++] = cur; stack[stk_top++] = NULL; }else{ cur = stack[--stk_top]; res[(*returnSize)++] = cur->val; } } return res; }
中序遍历先处理的是左节点,因而其入栈顺序为
右-根-NULL-左.实现代码如下:
int* inOrderTraverse2(BinaryTree *root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; stack[stk_top++] = root; while(stk_top != 0){ BinaryTree* cur = stack[--stk_top]; if(cur){ if(cur->rChild) stack[stk_top++] = cur->rChild; stack[stk_top++] = cur; stack[stk_top++] = NULL; if(cur->lChild) stack[stk_top++] = cur->lChild; }else{ cur = stack[--stk_top]; res[(*returnSize)++] = cur->val; } } return res; }
后序遍历先处理的是左节点,因而其入栈顺序为
根-NULL-右-左.实现代码如下:
int* postOrderTraverse2(BinaryTree *root, int *returnSize){ if(!root) return NULL; int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM); BinaryTree* stack[MAX_NODE_NUM]; int stk_top = 0; *returnSize = 0; stack[stk_top++] = root; while(stk_top != 0){ BinaryTree* cur = stack[--stk_top]; if(cur){ stack[stk_top++] = cur; stack[stk_top++] = NULL; if(cur->rChild) stack[stk_top++] = cur->rChild; if(cur->lChild) stack[stk_top++] = cur->lChild; }else{ cur = stack[--stk_top]; res[(*returnSize)++] = cur->val; } } return res; }
3.3.6 二叉树ACM代码
#include <stdio.h> //printf,scanf
#include <stdlib.h> //malloc
//#include <string.h> //memset
#define MAX_NODE_NUM 100 //树的节点数最大为100
typedef struct MyBinaryTree {
int val;
struct MyBinaryTree *lChild;
struct MyBinaryTree *rChild;
}BinaryTree;
BinaryTree* ConstructTree(int *nums, int numsSize){
if(numsSize < 1) return NULL;
BinaryTree** nodes = (BinaryTree**)malloc(sizeof(BinaryTree*)*numsSize);
for(int i = 0; i < numsSize; ++i){
if(nums[i] == -1){
nodes[i] = NULL;
}else{
nodes[i] = (BinaryTree*)malloc(sizeof(BinaryTree));
nodes[i]->val = nums[i];
nodes[i]->lChild = NULL;
nodes[i]->rChild = NULL;
}
}
BinaryTree *root = nodes[0];
for(int i = 0; 2*i+2 < numsSize; ++i){
if(!nodes[i]){
continue;
}
nodes[i]->lChild = nodes[2*i+1];
nodes[i]->rChild = nodes[2*i+2];
}
return root;
}
/***********************************一般遍历****************************************/
int* preOrderTraverse(BinaryTree* root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
BinaryTree* cur = root;
while(cur || stk_top != 0){
while(cur){
stack[stk_top++] = cur;
res[(*returnSize)++] = cur->val;
cur = cur->lChild;
}
cur = stack[--stk_top];
cur = cur->rChild;
}
return res;
}
int* inOrderTraverse(BinaryTree* root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
BinaryTree* cur = root;
while(cur || stk_top != 0){
while(cur){
stack[stk_top++] = cur;
cur = cur->lChild;
}
cur = stack[--stk_top];
res[(*returnSize)++] = cur->val;
cur = cur->rChild;
}
return res;
}
void reverse(int **res, int l, int r){
while(l < r){
int num = (*res)[l];
(*res)[l++] = (*res)[r];
(*res)[r--] = num;
}
}
int* postOrderTraverse(BinaryTree* root, int *returnSize){ //根-右-左然后翻转一下
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
BinaryTree* cur = root;
while(cur || stk_top != 0){
while(cur){
stack[stk_top++] = cur;
res[(*returnSize)++] = cur->val;
cur = cur->rChild;
}
cur = stack[--stk_top];
cur = cur->lChild;
}
reverse(&res, 0, *returnSize-1);
return res;
}
//层序遍历
int* layerTraverse(BinaryTree* root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* queue[MAX_NODE_NUM];
int front = 0, rear = 0;
*returnSize = 0;
queue[rear++] = root;
while(front != rear){
int size = rear - front;
while(size--){
BinaryTree* cur = queue[front++];
res[(*returnSize)++] = cur->val;
if(cur->lChild) queue[rear++] = cur->lChild;
if(cur->rChild) queue[rear++] = cur->rChild;
}
}
return res;
}
/***********************************统一迭代****************************************/
int* preOrderTraverse2(BinaryTree *root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
stack[stk_top++] = root;
while(stk_top != 0){
BinaryTree* cur = stack[--stk_top];
if(cur){
if(cur->rChild) stack[stk_top++] = cur->rChild;
if(cur->lChild) stack[stk_top++] = cur->lChild;
stack[stk_top++] = cur;
stack[stk_top++] = NULL;
}else{
cur = stack[--stk_top];
res[(*returnSize)++] = cur->val;
}
}
return res;
}
int* inOrderTraverse2(BinaryTree *root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
stack[stk_top++] = root;
while(stk_top != 0){
BinaryTree* cur = stack[--stk_top];
if(cur){
if(cur->rChild) stack[stk_top++] = cur->rChild;
stack[stk_top++] = cur;
stack[stk_top++] = NULL;
if(cur->lChild) stack[stk_top++] = cur->lChild;
}else{
cur = stack[--stk_top];
res[(*returnSize)++] = cur->val;
}
}
return res;
}
int* postOrderTraverse2(BinaryTree *root, int *returnSize){
if(!root) return NULL;
int *res = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
BinaryTree* stack[MAX_NODE_NUM];
int stk_top = 0;
*returnSize = 0;
stack[stk_top++] = root;
while(stk_top != 0){
BinaryTree* cur = stack[--stk_top];
if(cur){
stack[stk_top++] = cur;
stack[stk_top++] = NULL;
if(cur->rChild) stack[stk_top++] = cur->rChild;
if(cur->lChild) stack[stk_top++] = cur->lChild;
}else{
cur = stack[--stk_top];
res[(*returnSize)++] = cur->val;
}
}
return res;
}
/***********************************递归实现****************************************/
void preOrderTraverse3(BinaryTree *root, int *res, int *returnSize){
if(!root) return;
res[(*returnSize)++] = root->val;
preOrderTraverse3(root->lChild, res, returnSize);
preOrderTraverse3(root->rChild, res, returnSize);
}
void inOrderTraverse3(BinaryTree *root, int *res, int *returnSize){
if(!root) return;
inOrderTraverse3(root->lChild, res, returnSize);
res[(*returnSize)++] = root->val;
inOrderTraverse3(root->rChild, res, returnSize);
}
void postOrderTraverse3(BinaryTree *root, int *res, int *returnSize){
if(!root) return;
postOrderTraverse3(root->lChild, res, returnSize);
postOrderTraverse3(root->rChild, res, returnSize);
res[(*returnSize)++] = root->val;
}
//将遍历结果打印出来
void display(int* nums, int numsSize){
for(int i = 0; i < numsSize; ++i){
if(i && i%5==0) printf("\n");
printf("%3d", nums[i]);
}
printf("\n");
}
//遍历函数
void traverse(BinaryTree* root, int numsSize){
int size = 0;
printf("先序遍历1结果:\n");
int *preOrder = preOrderTraverse(root, &size);
display(preOrder, size);
//printf("先序遍历2结果:\n");
//int *preOrder2 = preOrderTraverse2(root, &size);
//display(preOrder2, size);
//printf("先序遍历3结果:\n");
//size = 0;
//int *preOrder3 = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
//preOrderTraverse3(root, preOrder3, &size);
//display(preOrder3, size);
printf("中序遍历1结果:\n");
int *inOrder = inOrderTraverse(root, &size);
display(inOrder, size);
//printf("中序遍历2结果:\n");
//int *inOrder2 = inOrderTraverse2(root, &size);
//display(inOrder2, size);
//printf("中序遍历3结果:\n");
//size = 0;
//int *inOrder3 = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
//inOrderTraverse3(root, inOrder3, &size);
//display(inOrder3, size);
printf("后序遍历1结果:\n");
int *postOrder = postOrderTraverse(root, &size);
display(postOrder, size);
//printf("后序遍历2结果:\n");
//int *postOrder2 = postOrderTraverse2(root, &size);
//display(postOrder2, size);
//printf("后序遍历3结果:\n");
//size = 0;
//int *postOrder3 = (int *)malloc(sizeof(int)*MAX_NODE_NUM);
//postOrderTraverse3(root, postOrder3, &size);
//display(postOrder3, size);
printf("层序遍历结果:\n");
int *layer = layerTraverse(root, &size);
display(layer, size);
}
int main(){
int nums[MAX_NODE_NUM];
int index = 0;
printf("请输入二叉树的节点值(-1表示该节点为空),按空格结束输入\n");
while(1){
int num;
scanf("%d", &num);
char ch = getchar();
nums[index++] = num;
if(ch == '\n' || index == MAX_NODE_NUM) break;
}
BinaryTree* root = ConstructTree(nums, index);
traverse(root, index);
// free(nums);
free(root);
return 0;
} 3.3.7 二叉搜索树
- 插入
BST插入结点只需要按照BST的性质寻找插入位置即可。
- 当待插入的树为空树时,直接将待插入节点作为根节点返回即可。
- 当待插入的树不为空时,按照BST性质查找位置:
- 当待插入节点的值小于当前节点值时,则插入位置在当前节点的左子树中。
- 当待插入节点的值大于当前节点值时,则插入位置在当前节点的右子树中。
- 当待插入节点的值等于当前节点值时,插入失败。
具体实现:
bool insert(struct TreeNode* root, int val){
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->val = val;
if(!root){ //空树直接作为根节点即可
root = node;
return true;
}
TreeNode *cur = root, *parent = NULL;
while(cur){ //查找插入位置
parent = cur;
if(cur->val < val){
cur = cur->right;
}else if(cur->val > val){
cur = cur->left;
}else{
return false;
}
}
if(parent->val > val){ //判断插入位置在左还是在右
parent->left = node;
}else{
parent->right = node;
}
return true;
}- 删除
删除操作相对插入操作较为复杂。首先需要查找待删除节点位置,如果节点不在树中,则返回false表明删除失败即可。当找到待插入节点的位置时,有以下三种情况:
- 待删除结点的左子树为空:将该节点的双亲结点指向其的指针改为指向其右子树,然后将该节点释放即可。
- 待删除结点的右子树为空:将该节点的双亲结点指向其的指针改为指向其左子树,然后将该节点释放即可。
- 待删除结点的左右子树均不为空:将该节点的值修改为其左子树中最大值或右子树中最小值,并将对应的结点删去即可。
具体实现:
bool delete(struct TreeNode* root, int val){
if(!root) return false;
struct TreeNode* cur = root, *parent = NULL;
while(cur){
if(cur->val == val){
break;
}else if(cur->val < val){
parent = cur;
cur = cur->right;
}else{
parent = cur;
cur = cur->left;
}
}
if(!cur) return false;
if(!cur->left){ // 第一种情况
if(parent->val < val){
parent->right = cur->right;
}else{
parent->left = cur->right;
}
free(cur);
}else if(!cur->right){ // 第二种情况
if(parent->val < val){
parent->right = cur->left;
}else{
parent->left = cur->left;
}
free(cur);
}else{ // 第三种情况
struct TreeNode* cur1 = cur->right;
while(cur1->left){
parent = cur1;
cur1 = cur1->left;
}
cur->val = cur1->val;
if(parent->right == cur1) {
parent->right = cur1->right;
}else {
parent->left = cur1->right;
}
free(cur1);
}
return true;
} 3.4 哈希表
3.4.1 简介
c语言本身没有哈希,需要使用第三方头文件uthash.h.
Entry:键值对,key-value,其中key为元素的值
哈希表的扩容:增长因子/负载因子,已占内存与总内存的百分比,当达到该阈值时,就触发扩容机制。
HashMap的增长因子为75%。
扩容机制:新建一个原数组的2倍大小的数组,并将原数组中的entry重新hash一遍
3.4.2 结构体定义
typedef struct {
ElemType key; //键值
//ElemType val; //其他有用的数据,如数量等
UT_hash_handle hh; //哈希函数处理句柄,声明时必须有这一句否则报错
}HashTable, HashMap; 3.4.3 哈希操作
struct hashTable *users = NULL; //一定要初始化为NULL,不然会报错.
HASH_FIND_INT(users, &data, tmp); //查询, users为待查询的哈希表,&user_key为目标key的地址,tmp为函数输出值
HASH_ADD_INT(users, key, tmp); //插入,users为待插入的哈希表,key为key域的变量名,tmp为待插入的entry结构体
HASH_COUNT(users); //统计,users为待查询的哈希表,输出值为哈希表中entry个数
HASH_DEL(users, tmp); //将哈希表user中的tmp删去 哈希表的遍历有两种方式,一种是内置的HASH_ITER函数,另一种则是采用for循环,利用结构体内置的哈希处理句柄hh进行。
方式1
/*遍历,hh为hash句柄,users为待循环的哈希表,s为每次遍历的entry, /tmp临时变量(好像没啥用但一定要有,并且需要提前定义,但不需要初始化)*/ struct my_struct *s, *tmp; HASH_ITER(hh, users, s, tmp) { printf("user id %d: name %s\n", s->id, s->name); /* ... it is safe to delete and free s here */ }方式2
void print_users() { struct my_struct *s; for(s=users; s != NULL; s=s->hh.next) { printf("user id %d: name %s\n", s->id, s->name); } }
3.5 堆
4 常规算法
4.1 二分法
4.2 动态规划
4.3 贪心算法
4.4 回溯
4.5 KMP
4.6 排序
4.7 bfs/dfs
5 va_list
4.1 二分法
4.2 动态规划
4.3 贪心算法
4.4 回溯
4.5 KMP
4.6 排序
4.7 bfs/dfs
5 va_list
4.3 贪心算法
4.4 回溯
4.5 KMP
4.6 排序
4.7 bfs/dfs
5 va_list
4.5 KMP
4.6 排序
4.7 bfs/dfs
5 va_list
4.7 bfs/dfs
5 va_list
va_list是针对变参问题的一组系统宏,实现函数参数不定的功能。C语言中利用省略号来表示不定长参数:void func(int a,...), 注意, c标准规定了函数必须至少有一个明确定义的参数,因而省略号前至少要有一个类型已知的参数。
va_list: 宏定义了一个指向参数列表中的参数的指针类型void va_start(va_list ap, param1): 获取可变参数列表的第一个参数的地址(ap是类型为va_list的指针,param1是可变参数最左边的参数)Elemtype va_arg(va_list, Elemtype): 获取参数列表的下一个参数,并以type的类型返回。void va_end(va_list ap): 参数列表访问完以后,参数列表指针与其他指针一样,必须收回,否则出现野指针,可理解为清空va_list可变参数列表。一般va_start和va_end配套使用。_vsnprintf: 用于向字符串中打印数据、数据格式用户自定义.int _vsnprintf(char* str, size_t size, const char* format, va_list ap);char *str [out],把生成的格式化的字符串存放在这里.size_t size [in], str可接受的最大字符数 (非字节数,UNICODE一个字符两个字节),防止产生数组越界.const char *format [in], 指定输出格式的字符串,它决定了你需要提供的可变参数的类型、个数和顺序。va_list ap [in],va_list变量.va:variable-argument:可变参数
c++的目录
0.各种基础知识
1.类
0 各种基础知识
C是结构化和模块化的语言,是面对过程的;C++则是在C的基础上增加了面向对象的机制。
- 结构化:主要使用顺序、选择、循环三种基本结构,核心是将程序模块化。
- 面向对象:程序以“对象”为中心进行分析和设计的。先将问题空间划分为一系列对象的集合,再将对象集合进行分类抽象,一些具有相同属性行为的对象被抽象为一个类,类还可抽象分为子类、超类(超类是子类的抽象)。采用继承来建立这些类之间的联系,形成结构层次。
iostream.h: 类似C语言中的stdio.h,但后者不能重载,而前者则可以通过运算符重载机制对iostream库进行扩充。
- 熟悉的输入输出操作分别是由istream(输入流)和ostream(输出流)这两个类提供的,为了允许双向的输入/输出,由istream和ostream派生出了iostream类。
- iostream库定义了以下三个标准流对象:
- cin,表示标准输入(standard input)的istream类对象。cin使我们可以从设备读入数据。
- cout,表示标准输出(standard output)的ostream类对象。cout使我们可以向设备输出或者写数据。
- cerr,表示标准错误(standard error)的osttream类对象。cerr是导出程序错误消息的地方,它只能允许向屏幕设备写数据。
- 输出主要由重载的左移操作符(<<)来完成,输入主要由重载的右移操作符(>>)完成:
>>a表明将数据放入对象a中;<<a则是将a对象中存储的数据拿出。
#include <iostream.h>
int main{
char name[10];
cout<<"请输入你的名字:";
cin>>name[10];
cout<<"Hello World!"<<endl; //end为换行符,作用同'\n'
return 0;
}
标识符必须以字母或下划线开头,且区分大小写;标识符长度一般不超过31个,超过时若前32个一样则会被认为是相同的标识符。
const修饰的变量限制了用户将其作为左值进行赋值操作。将其地址传给函数可以进行修改,但是C里边会warning,c++的待尝试。
int在16位机为4字节,32/64位机位8字节;long跟int是一样的,long long则是16字节。float为4字节,double为8字节,long double为10字节。进行运算时,float和double会进行四舍五入,而整型则是舍弃小数部分。
十进制直接为数字,八进制以’0’开头,十六进制以’0X’或’0x’开头。
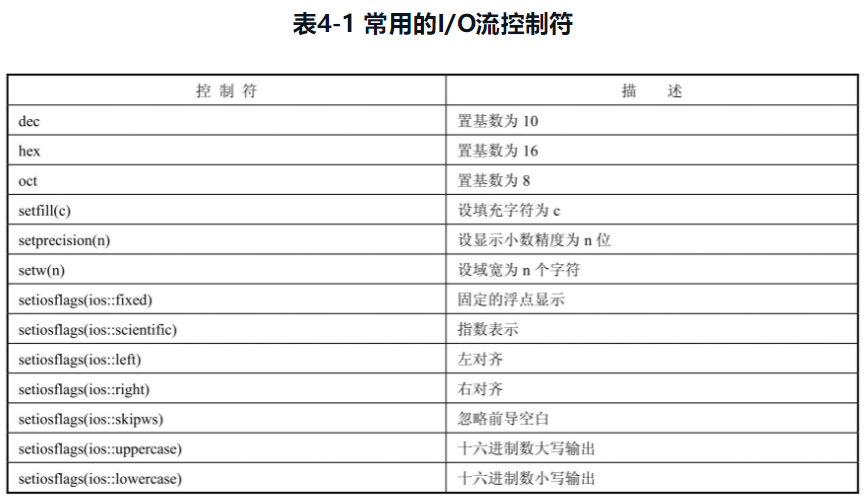
#include <iostream.h>
void main{
int a = 100;
double b = 1.23456789;
cout<<"默认下:"<<a<<endl; //默认输出进制
cout<<"十进制下:"<<dec<<a<<endl; //输出十进制
cout<<"八进制下:"<<oct<<a<<endl; //输出八进制
cout<<"十六进制下:"<<hex<<a<<endl; //输出十六进制
cout<<setw(10)<<a<<endl; //输出宽度为10(不足位则右对齐)
cout<<setprecision(3)<<b<<endl; //输出精度为3(即有效位,默认为6)(四舍五入)
}
1.类
0 各种基础知识
C是结构化和模块化的语言,是面对过程的;C++则是在C的基础上增加了面向对象的机制。
- 结构化:主要使用顺序、选择、循环三种基本结构,核心是将程序模块化。
- 面向对象:程序以“对象”为中心进行分析和设计的。先将问题空间划分为一系列对象的集合,再将对象集合进行分类抽象,一些具有相同属性行为的对象被抽象为一个类,类还可抽象分为子类、超类(超类是子类的抽象)。采用继承来建立这些类之间的联系,形成结构层次。
iostream.h: 类似C语言中的stdio.h,但后者不能重载,而前者则可以通过运算符重载机制对iostream库进行扩充。
- 熟悉的输入输出操作分别是由istream(输入流)和ostream(输出流)这两个类提供的,为了允许双向的输入/输出,由istream和ostream派生出了iostream类。
- iostream库定义了以下三个标准流对象:
- cin,表示标准输入(standard input)的istream类对象。cin使我们可以从设备读入数据。
- cout,表示标准输出(standard output)的ostream类对象。cout使我们可以向设备输出或者写数据。
- cerr,表示标准错误(standard error)的osttream类对象。cerr是导出程序错误消息的地方,它只能允许向屏幕设备写数据。
- 输出主要由重载的左移操作符(<<)来完成,输入主要由重载的右移操作符(>>)完成:
>>a表明将数据放入对象a中;<<a则是将a对象中存储的数据拿出。
#include <iostream.h>
int main{
char name[10];
cout<<"请输入你的名字:";
cin>>name[10];
cout<<"Hello World!"<<endl; //end为换行符,作用同'\n'
return 0;
}标识符必须以字母或下划线开头,且区分大小写;标识符长度一般不超过31个,超过时若前32个一样则会被认为是相同的标识符。
const修饰的变量限制了用户将其作为左值进行赋值操作。将其地址传给函数可以进行修改,但是C里边会warning,c++的待尝试。
int在16位机为4字节,32/64位机位8字节;long跟int是一样的,long long则是16字节。float为4字节,double为8字节,long double为10字节。进行运算时,float和double会进行四舍五入,而整型则是舍弃小数部分。
十进制直接为数字,八进制以’0’开头,十六进制以’0X’或’0x’开头。
#include <iostream.h>
void main{
int a = 100;
double b = 1.23456789;
cout<<"默认下:"<<a<<endl; //默认输出进制
cout<<"十进制下:"<<dec<<a<<endl; //输出十进制
cout<<"八进制下:"<<oct<<a<<endl; //输出八进制
cout<<"十六进制下:"<<hex<<a<<endl; //输出十六进制
cout<<setw(10)<<a<<endl; //输出宽度为10(不足位则右对齐)
cout<<setprecision(3)<<b<<endl; //输出精度为3(即有效位,默认为6)(四舍五入)
}
类型转换包括隐式转换和显示转换。
运算符的优先级
- 第一级:小括号【()】、中括号【[]】、分量运算符的指向结构体成员运算符【->】、结构体成员运算符【.】;
- 第二级:逻辑非【!】、按位取反【~】、单目运算【++, —】、负号运算符【-】、类型转换【(ElemType)】、指针运算符和取地址运算符【*, &】、长度运算符【sizeof】、动态存储分配【new, delete】(注:逻辑非高于单目运算);
- 第三级:【*, /】、【%】;
- 第四级:【+, -】;
- 第五级:【>>】、【<<】;
- 第六级:【<, >, <=, >=】;
- 第七级:【==, !=】;
- 第八级:【&】;
- 第九级:【^】;
- 第十级:【|】;
- 第十一级:【&&】;
- 第十二级:【||】;
- 第十三级:条件/三目运算符【? :】;
- 第十四级:(复合)赋值运算符;
- 第十五级:【,】;
do...while和while的区别:前者先进行循环,而后再进行条件的判断,因而最少循环一次;后者则是先进行条件的判断,因此循环可能不进行。函数的属性说明可以缺省,一般为inline(内联函数)、static(静态函数)、virtual(虚函数)、friend(友元函数)等。
main函数本身也可以带参数,声明如下:
int main(int argc, char *argv[])其中,argc表示命令行中字符串的个数,指针数组argv[]指向命令行中的各个字符串。可以用其他标识符命名,但顺序与参数类型不可改变。
C++中可以对函数中形参进行初始化,调用函数时如果没有对该形参给出对应的实参,则函数将按默认值进行工作。形参的默认值必须要在声明中指定,而不能在定义中指定,并且默认值的定义必须遵守从右到左的顺序,即若某个参数没有默认值,则其左侧的参数就不能有默认值。
函数重载是指同一个函数名可以对应着多个函数的实现。函数重载又称为函数的多态性,是指同一个函数名对应着多个不同的函数。所谓“不同”是指这些函数的形参表必须互不相同,或者是形参的个数不同,或者是形参的类型不同,或者是两者都不相同,否则将无法实现函数重载。重载函数的类型,即函数的返回类型,可以相同,也可以不同。但如果仅仅是返回类型不同而函数名相同、形参表也相同,则是不合法的。
C++中的排序sort默认是从小到大排序,如果要从大到小排序,可以重写comp函数,类似于C中qsort()里的compare(), 实现方法:
一维vector
//第一种写法: lambda表达 sort(vec.begin(), vec.end(), [](const int a, const int b){ return a > b; }); //第二种写法:自定义函数对象 class comp(){ public: bool operator()(int a, int b){ return a > b; } } sort(vec.begin(), vec.end(), comp()); //第三种写法 sort(vec.begin(), vec.end(), std::greater<int>());多维vector
//第一种写法: lambda表达 sort(vec.begin(), vec.end(), [](const vector<int>a, const vector<int>b){ return a[1] > b[1]; }); //第二种写法:自定义函数对象 class comp(){ public: bool operator()(vector<int> a, vector<int> b){ return a[1]>b[1]; } } sort(vec.begin(), vec.end(), comp()); ``` # <h3> 1 <span id="ClassofCpp">类</span> # <h4> 1.1 从结构体到类 - 定义一个简单的结构体如下: ```cpp #include <iostream.h> struct point{ //定义结构体 int x; //定义成员变量 int y; }; void main{ point pt; //定义结构体变量 pt.x = 5; //引用成员变量并赋值 pt.y = 3; cout<<"pt.x = "<<pt.x<<endl; //输出 cout<<"pt.y = "<<pt.y<<endl; }上述代码实现的功能是输出结体变量的成员变量的值,等效于下面的代码:
#include <iostream.h>
struct point{ //定义结构体
int x; //定义成员变量
int y;
void print(){ //定义成员函数
cout<<"x = "<<x<<endl; //输出
cout<<"y = "<<y<<endl;
}
};
void main{
point pt; //定义结构体变量
pt.x = 5; //引用成员变量并赋值
pt.y = 3;
pt.print(); //引用成员函数
}调用结构体函数时,其后的小括号不能缺省!!!
对以上的代码中结构体的定义进行修改,将struct关键字更换为class关键字,完成从结构体到类的转变:
#include <iostream.h>
class point{ //声明类
int x; //定义成员变量
int y;
void print(){ //定义成员函数
cout<<"x = "<<x<<endl; //输出
cout<<"y = "<<y<<endl;
}
};
void main{
point pt; //定义结构体变量
pt.x = 5; //引用成员变量并赋值
pt.y = 3;
pt.print(); //引用成员函数
}注意,结构体中的变量默认是公有(public)的,定义了结构变量则可以对其成员变量进行访问。
而类的变量则默认是私有(private)的。公有成员在类外可以进行访问,而私有成员只能在类中访问,在类外访问则报错。
从这可以看出,结构体和类除了关键字的区别,更重要的是成员访问控制的差异。
- 类的声明:
class <ClassName> {
private:
私有函数和数据
public:
受保护数据和函数
}; //与结构体类似,类的定义也是以分号结束1.2 构造函数
- 定义类成员变量时不能对其进行初始化,即不能在类中声明变量时手动进行赋值,而是需要借助构造函数来实现。
构造函数:是在类中定义的一种特殊函数,其函数名与类名一致,功能是为类中变量分配空间和初始赋值,不能用关键字进行修饰(void, int等),更不能有return语句。构造函数同样属于类中的成员函数,可以访问所有成员变量。
class complex {
private:
double real; //类的成员变量
double imag;
public:
complex(double r, double i); //声明类的构造函数
void print(){ //类的成员函数
cout<<real<<"+"<<imag<<"i"<<endl;
}
}
complex::complex(double r, double i){ //定义类的构造函数
real = r;
imag = i;
}
void main() {
complex ops1(1.2, 3.0);
ops1.print();
}在类外对类的成员函数进行定义时需要在函数名前加类名和域运算符”::”,即<类名>::<函数名>(参数表).
1.3 拷贝构造函数
作用:通过已存在的对象来对该类的新对象进行初始化
定义:
类名(类名&对象名){
函数体
}
1.4 析构函数
- 作用:释放分配给成员变量的内存空间
- 定义:与构造函数类似,但没有参数表,且函数名前加上“~”.
每个类必须要有析构函数,但大多情况下默认生成的析构函数即可满足需求,当需要在函数体内进行自定义操作时才需要自定义析构函数。通常情况下,构造函数中使用”new”来申请内存空间,析构函数中用”delete”来释放内存。
1.5 友元函数
作用:提供了不同类或对象的成员函数之间、类的成员函数与一般函数之间的共享机制。
独立于当前类的外部函数,可以访问类所有对象的所有成员。
定义:
friend <函数类型> <函数名>(参数表);
2 继承
3 iterator迭代器
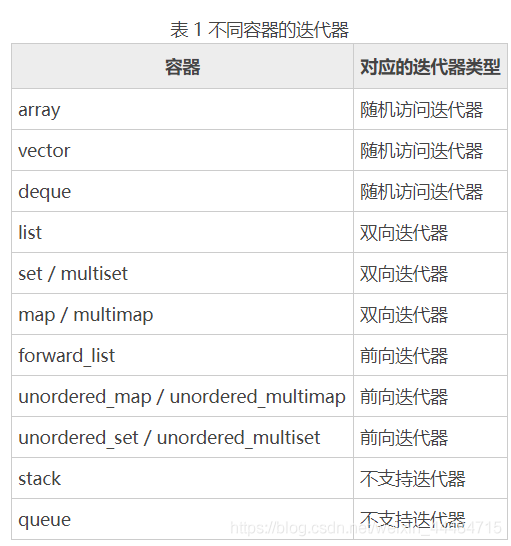
前向迭代器
假设 p 是一个前向迭代器,则 p 支持 ++p,p++,*p 操作,还可以被复制或赋值,可以用 == 和 != 运算符进行比较。此外,两个正向迭代器可以互相赋值。
双向迭代器
双向迭代器具有正向迭代器的全部功能,除此之外,假设 p 是一个双向迭代器,则还可以进行 —p 或者 p— 操作(即一次向后移动一个位置)。
随机访问迭代器
随机访问迭代器具有双向迭代器的全部功能。除此之外,假设 p 是一个随机访问迭代器,i 是一个整型变量或常量,则 p 还支持以下操作:
- p+=i:使得 p 往后移动 i 个元素。
- p-=i:使得 p 往前移动 i 个元素。
- p+i:返回 p 后面第 i 个元素的迭代器。
- p-i:返回 p 前面第 i 个元素的迭代器。
- p[i]:返回 p 后面第 i 个元素的引用。
- 此外,两个随机访问迭代器 p1、p2 还可以用 <、>、<=、>= 运算符进行比较。另外,表达式 p2-p1 也是有定义的,其返回值表示 p2 所指向元素和 p1 所指向元素的序号之差(也可以说是 p2 和 p1 之间的元素个数减一)。
4 vector容器
Vector是一个封装了动态大小数组的顺序容器(sequence container),能够存放任意类型的对象的动态数组。Vector支持对序列中的任意元素进行快速直接访问,甚至可以通过指针算述进行该操作。提供了在序列末尾相对快速地添加/删除元素的操作。
4.1 特性
内存自增长:与其他容器不同,其内存空间只会增长,不会减小。对vector,必有vec.capacity() >= vec.size(),前者是容器所能存储的元素个数,后者则是容器内当前存储的元素个数。每当vector容器不得不分配新的存储空间时,会以加倍当前容量的分配策略实现重新分配。
reserve()成员可以用来控制容器的预留空间,如reserve(10)则是预留10个元素空间
释放空间:vector<int>().swap(nums);或nums.swap(vector<int> ());
swap()是交换函数,使vector离开其自身的作用域,从而强制释放vector所占的内存空间.
如nums为类中成员,则不能把vector<int>().swap(nums);写入折构函数中,而应:
>void clearVector( vector<T>& vt){
vector<T> vtTemp;
vtTemp.swap(vt);
>}
4.2 基本操作
创建vector对象:vector<int> vec;//一维数组
vector<vector<int> > vec(n, vector<int>(m));//二维数组,行数为n,列数为m
尾部插入数字a:vec.push_back(a);
使用下标访问元素:cout<<vec[i]<<endl;
使用迭代器访问元素
vector<int>::iterator it;//声明一个迭代器,来访问vector容器,作用:遍历或者指向vector容器的元素
for(it=obj.begin();it!=obj.end();it++)
{
cout<<*it<<" ";
}
在第i个位置插入元素:vec.insert(vec.begin()+i, a);
删除尾部元素: vec.pop_back();
删除第i个元素: vec.erase(vec.begin()+i);
向量大小:vec.size();
清空: vec.clear();
排序:sort(vec.begin(), vec.end());//从小到大排序
sort()需要头文件#inlcude <algorithm>
如需从大到小排序,则重定义比较函数bool comp(const int &a, const int &b) return a > b;,并在sort中进行调用sort(vec.begin(),vec.end(),comp)
反转:reverse(vec.begin(), vec.end());
5 Map/Set容器
- Map:提供一对一(其中第一个可以称为关键字,每个关键字只能在map中出现一次,第二个可能称为该关键字的值)的数据处理能力。map内部自建一颗红黑树(一 种非严格意义上的平衡二叉树),这颗树具有对数据自动排序的功能。
内存自增长:与其他容器不同,其内存空间只会增长,不会减小。对vector,必有vec.capacity() >= vec.size(),前者是容器所能存储的元素个数,后者则是容器内当前存储的元素个数。每当vector容器不得不分配新的存储空间时,会以加倍当前容量的分配策略实现重新分配。
reserve()成员可以用来控制容器的预留空间,如
reserve(10)则是预留10个元素空间
释放空间:vector<int>().swap(nums);或nums.swap(vector<int> ());
swap()是交换函数,使vector离开其自身的作用域,从而强制释放vector所占的内存空间.
如nums为类中成员,则不能把vector<int>().swap(nums);写入折构函数中,而应:>void clearVector( vector<T>& vt){ vector<T> vtTemp; vtTemp.swap(vt); >}
4.2 基本操作
创建vector对象:
vector<int> vec;//一维数组
vector<vector<int> > vec(n, vector<int>(m));//二维数组,行数为n,列数为m尾部插入数字a:
vec.push_back(a);使用下标访问元素:
cout<<vec[i]<<endl;使用迭代器访问元素
vector<int>::iterator it;//声明一个迭代器,来访问vector容器,作用:遍历或者指向vector容器的元素 for(it=obj.begin();it!=obj.end();it++) { cout<<*it<<" "; }在第i个位置插入元素:
vec.insert(vec.begin()+i, a);删除尾部元素:
vec.pop_back();删除第i个元素:
vec.erase(vec.begin()+i);向量大小:
vec.size();清空:
vec.clear();排序:
sort(vec.begin(), vec.end());//从小到大排序sort()需要头文件
#inlcude <algorithm>
如需从大到小排序,则重定义比较函数bool comp(const int &a, const int &b) return a > b;,并在sort中进行调用sort(vec.begin(),vec.end(),comp)反转:
reverse(vec.begin(), vec.end());
5 Map/Set容器
- Map:提供一对一(其中第一个可以称为关键字,每个关键字只能在map中出现一次,第二个可能称为该关键字的值)的数据处理能力。map内部自建一颗红黑树(一 种非严格意义上的平衡二叉树),这颗树具有对数据自动排序的功能。
5.1 Map操作
- 定义:
std::map <int, string> map; //创建key为int类型,并拥有相关联的指向string的指针- 数据的插入
- 用insert插入pair数据
map.insert(pair<int, string>(1, "STRING"));- 用insert插入value_type数据
map.insert(map<int, string>::value_type (1, "STRING")); - 用数组形式插入
map<int, string> map;
map[1] = "STRING1";
map[2] = "STRING2";- 多值插入
map.insert(nums.begin(), nums.end());- 遍历
- 迭代器
迭代器:类似于C里边的指针,用于访问顺序容器和关联容器中的元素. 分为正向迭代器和反向迭代器,前者定义为
容器类名::iterator 迭代器名;,后者定义为容器类名::reverse_iterator 迭代器名;。前者为正向遍历,即从容器的begin开始遍历到end,而后者则是从end前一个元素遍历到begin. - 数组
- 查找
- count: 若存在则返回1,否则返回0
- find: 返回一个迭代器,如果存在则返回该元素所在未知的迭代器,否则返回end函数返回的迭代器
- 删除
- 采用迭代器进行删除
map<int, string>::interator iter;
iter = map.find(1);
map.erase(iter);- 采用关键字进行删除
int n = map.erase(1); //如果删除了则返回1,否则返回0- 删除一个范围
map.erase(map.begin(), map.end()); 6 栈
7 链表(双向)
- 插入:
insert(): 插入后迭代器位于插入元素的位置上,而原来的迭代器上的元素以及后继节点则均后移一位.insert(it, elem): 在迭代器it的位置上插入新节点,节点元素为elem.insert(it, n, elem): 在迭代器it的位置上连续插入n个elem元素.
emplace: 直接构造emplace_back(elem): 在链表的末尾插入元素elem.emplace_front(elem): 在链表的第一个元素前头插入元素elem.emplace(it, elem): 同insert(it, elem).
删除:
clear(): 清除链表中的所有元素remove(val): 清除链表中所有val的节点remove_if(): 清楚满足条件的节点unique(): 清楚链表中相邻位置相同的节点,仅保留第一个节点erase(): 删除list容器中指定位置处的元素(erase(it)),也可以删除容器中某一段的多个元素(erase(it1, it2))pop_back(): 删除链表末尾节点pop_front(): 删除链表起始节点remove_if使用示例:>#include <iostream> >#include <list> >using namespace std; >bool odd(int n) {return n%2;} >void main(){ list<int> l = {1,2,3,4,5,6,7,8,9}; l.remove_if(odd); >}
- 反转/排序:
sort()reverse()
- 移动:
advance(it, n): 将迭代器it后移n位,为负则向前移,无返回值.prev(it, n): 与上边的功能类似,n为正则前移,为负则后移,缺省则为1即前移一位, 函数返回的结果为新的迭代器.next(it, n): 与advance一致,但与prev一样有返回值.这里的移动函数实际上都是
STL标准库中的迭代器辅助函数,定义于<iterator>头文件中并位于std命名空间中.advance和next可以采用任意的迭代器,而prev只能用双向迭代器和随机访问迭代器.- 前向迭代器:只可以作
it++和++it的操作. - 双向迭代器:除了可以作
++it、it++的操作,还可以作--it、it--的操作. - 随机访问迭代器:拥有双向迭代器的功能外,还可以进行
it+=n等操作.
- 前向迭代器:只可以作
- 其他:
distance(p, q): 返回迭代器p后移多少次后与迭代器q一致。iter_swap(p, q): 交换两个迭代器的值.
8 队列
- 队列(
queue)
- 双端队列(
deque)
deque 可以在常数时间内对队列的队头或队尾进行元素的插入与删除,是一种动态分段空间拼接而成的一种“容器”(注意是加了双引号)。
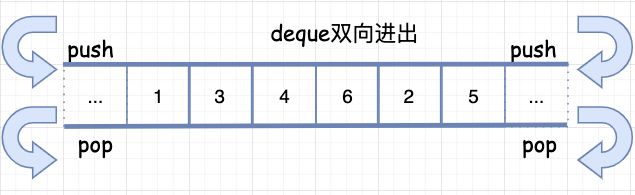
插入:deque可以在队头和队尾插入元素
push_back(elem): 在队尾加入元素push_front(elem): 在队头加入元素pop_back(): 删除队尾元素pop_front(): 删除队头元素insert(pos, elem): 在pos位置上插入元素并返回其地址insert(pos, n, elem): 在pos位置插入n个elem数据insert(pos,beg,end): 在pos位置插入[beg,end)区间的数据,无返回值。clear(): 清空容器的所有数据erase(beg,end): 删除[beg,end)区间的数据,返回下一个数据的位置。erase(pos): 删除pos位置的数据,返回下一个数据的位置。
读取
at(int idx): 返回索引idx所指的数据operator[]: 返回索引idx所指的数据front(): 返回容器中第一个数据元素back(): 返回容器中最后一个数据元素
容量
deque.empty(): 判断容器是否为空deque.size(): 返回容器中元素的个数deque.resize(num): 重新指定容器的长度为num,若容器变长,则以默认值填充新位置。如果容器变短,则末尾超出容器长度的元素被删除。deque.resize(num, elem): 重新指定容器的长度为num,若容器变长,则以elem值填充新位置。如果容器变短,则末尾超出容器长度的元素被删除。
- 优先队列(堆)
优先队列是一种抽象的数据类型,类似于常规的队列或栈, 但每个元素都有与之关联的“优先级”。在优先队列中, 低优先级的元素之前前面应该是高优先级的元素。如果两个元素具有相同的优先级, 则根据它们在队列中的顺序是它们的出现顺序即可。
C++的STL库queue中的优先队列priority_queue底层就是通过最小堆/最大堆来实现的
定义:
priority_queue<Type, Container, Functional>;, 其中Type为存放的数据类型,Container则是堆的底层容器(必须是数组类型,如vector、deque),而Functional则是比较函数/优先级。小顶堆:
priority_queue<int, vector<int>, greater<int>> q.- 大顶堆:
priority_queue<int, vector<int>, less<int>>.
Container缺省时为vector,Functional缺省是为大顶堆,即less<int>. 大顶堆排完序是从小到大,因而是less;而小顶堆排序后是从大到小,因而是greater.
重载
如果数据类型是自定义类型,因而不能直接采用
less<int>和greater<int>,即Functional不能缺省,需要重载operator <:strcut node{ int x, y; node(int x_, int y_): x(x_), y((y_){}; }; bool operator < (node a, node b){ if(a.x == b.x) return a.y > b.y; return a.x > b.x; }自定义cmp
struct cmp{ bool operator() ( Node a, Node b ){ if( a.x== b.x ) return a.y> b.y; return a.x> b.x; } }; int main(){ priority_queue<Node, vector<Node>, cmp> q; for( int i= 0; i< 10; ++i ) q.push( Node( rand(), rand() ) ); while( !q.empty() ){ cout << q.top().x << ' ' << q.top().y << endl; q.pop(); } getchar(); return 0; }
9 智能指针
Cpp中有四种智能指针:auto_tr, shared_ptr, weak_ptr, unique_ptr. 第一种已经被C++11弃用.
智能指针的作用就是为了更方便地管理动态内存。当采用new申请了一块动态内存,那么应该在函数结束时调用delete来释放该块内存,否则容易导致内存泄漏。但通过人为将new和delete配对来避免内存泄漏显然是低效的,而智能指针正是为了更好地管理指针。智能指针实际上是一个模板类,通过在类中创建目标对象,一旦超过智能指针地作用域时,则会自动调用析构函数来释放资源,从而避免内存泄漏。
- auto_ptr
auto_ptr可以通过成员函数get()来获取原始对象的指针,通过reset()函数来重新绑定指向的对象,而原来的对象将会被释放。而直接对智能指针进行赋值操作时,如ptest2 = ptest,那么ptest2将会接管ptest的内存管理权,且ptest将变为空指针;如果ptest2原本不为空,那么会先将ptest2指向的对象进行释放。
新版本的C++编译器已经将auto_ptr启用。
#include <iostream>
#include <memory>
using namespace std;
class Test{
...
public:
Test() {}
~Test() {}
...
void print();
}
int main(void) {
auto_ptr<Test> ptest1(new Test("123")); // 调用构造函数
auto_ptr<Test> ptest2(new Test("456"));
ptest1.get()->print(); // 获取原始指针并使用其指向的对象的成员函数
ptest2 = ptest1; // 释放ptest2指向的指针,然后将ptest1的内存管理权转给ptest2
if(ptest1.get() == NULL)
printf("ptest1 is NULL\n");
return 0; // 结束时自动释放两个指针,从而自动调用对象的析构函数
}- unique_ptr
unique_ptr是一个独享所有权的智能指针,提供了严格意义上的所有权,这也就意味着无法让两个unique_ptr来指向同一个对象。当本身被释放时,会使用给定的删除器释放它所指向的对象。
unique_ptr除了实现了auto_ptr的功能外,还增加了所有权移交的功能,即将unique_ptr作为函数参数传入函数时,会将内存管理权移交给参数(也可以说移交给了函数),而当函数返回时则可以将内存控制权重新移交给原来的unique_ptr。
注意,
unique_ptr不能采用ptest1 = ptest2的语句,否则就违反了独享所有权,如果要移交控制权,应该使用移动语义来实现:ptest1 = std::move(ptest2);
get(): 获取原始指针reset():重新绑定指向的对象,或者将删除原有的指针,这里只是删除智能指针,并未释放其指向的内存(后者无参数)release():相当于先调用get(),其次调用reset().
- shared_ptr
对象可以被多个shared_ptr所共享,即shared_ptr刚好和unique_ptr是反过来的。shared_ptr指向的对象除了可以通过new来构造,也可以通过传入auto_tr、unique_ptr、weak_ptr来构造。其共享机制是通过计数器的方式来实现的,当构造新的shared_ptr时计数器+1,当调用release函数时计数器-1,而当计数器为0时,资源将会被释放。
use_count(): 获取共享资源的shared_ptr个数swap(): 交换两个shared_ptr指向的对象
shared_ptr具体实现:
#include <iostream> #include <memory> #include <assert.h> template <typename T> class SmartPtr { private : T *_ptr; size_t *_count; public: SmartPtr(T *ptr = nullptr) : _ptr(ptr) { if (_ptr){ _count = new size_t(1); }else{ _count = new size_t(0); } } ~SmartPtr() { (*this->_count)--; if (*this->_count == 0) { delete this->_ptr; delete this->_count; } } SmartPtr(const SmartPtr &ptr) {// 拷贝构造:计数 +1 this->_ptr = ptr._ptr; this->_count = ptr._count; (*this->_count)++; } SmartPtr &operator=(const SmartPtr &ptr) { // 赋值运算符重载 if (this->_ptr == ptr._ptr) { return *this; } if (this->_ptr) {// 将当前的 ptr 指向的原来的空间的计数 -1 (*this->_count)--; if (*this->_count == 0) { delete this->_ptr; delete this->_count; } } this->_ptr = ptr._ptr; this->_count = ptr._count; (*this->_count)++; // 此时 ptr 指向了新赋值的空间,该空间的计数 +1 return *this; } T &operator*() { assert(this->_ptr != nullptr); return *(this->_ptr); } T *operator->() { assert(this->_ptr != nullptr); return this->_ptr; } size_t use_count() { return *this->count; } };
计数器用采用指针的形式,是希望对于指向相同对象的shared_ptr,都共享同一个计数器。和所有类对象共享一个变量不同,这里是限定了指向相同对象的类对象才共享这个变量,因而不能采用static,否则计数器就变成了程序中可用的shared_ptr的数量而不是共享某个对象资源的shared_ptr个数了。
- weak_ptr
weak_ptr 是一种不控制对象生命周期的智能指针, 它指向一个 shared_ptr 管理的对象. 进行该对象的内存管理的是那个强引用的 shared_ptr. weak_ptr只是提供了对管理对象的一个访问手段.
weak_ptr 设计的目的是为配合 shared_ptr 而引入的一种智能指针来协助 shared_ptr 工作, 它只可以从一个 shared_ptr 或另一个 weak_ptr 对象构造, 它的构造和析构不会引起引用记数的增加或减少.
使用shared_ptr时,当出现循环引用时,会导致内存泄漏,因为两个指针的计数器都不会为0,因而weak_ptr就是为了解决这个问题。
Python的目录
0.各种基础知识
1.random
0 各种基础知识
pass为空语句,保持程序结构的完整性,不做任何事情,一般用做占位语句。
zip():将对象中的元素打包为一个个tuple,并返回这些tuple所组成的list. 如zip(a, b, c, ...)(a,b,c均为数组)的作用是将每个数组对应位置上的元素打包作为一个向量,如果参数中的对象不等长,则按最短的长度进行”压缩”,超过长度的部分则被舍弃。
>>> a = ['a', 'b', 'c', 'd']
>>> b = ['1', '2', '3', '4']
>>> list(zip(a, b))
[('a', '1'), ('b', '2'), ('c', '3'), ('d', '4')]
1.random
0 各种基础知识
pass为空语句,保持程序结构的完整性,不做任何事情,一般用做占位语句。
zip():将对象中的元素打包为一个个tuple,并返回这些tuple所组成的list. 如
zip(a, b, c, ...)(a,b,c均为数组)的作用是将每个数组对应位置上的元素打包作为一个向量,如果参数中的对象不等长,则按最短的长度进行”压缩”,超过长度的部分则被舍弃。>>> a = ['a', 'b', 'c', 'd'] >>> b = ['1', '2', '3', '4'] >>> list(zip(a, b)) [('a', '1'), ('b', '2'), ('c', '3'), ('d', '4')]
zip()的逆操作:
result = zip(a, b)
origin = zip(*result) # 此处*号相当于解包运算符1 random
slice = random.sample(list, num):从列表list中随机抽取num个元素并通过slice返回

