深度强化学习

深度强化学习

Reinforcement Learning

1 Logistics回归（二分）

1.1 目标

通过对样本的特征向量与已有标签，训练得到线性函数，使得网络能够通过未知标签的样本的特征向量预测其标签，即使得下式成立：

$$\hat{y_i} = w^T x_i + b \approx y_i$$

，其中，$\hat{y_i}$为Logistics回归网络对样本$x_i$的标签的估计，而$y_i$则是样本$x_i$的实际标签。

由于Logistics回归是针对二分问题，所期望的输出是类别（通常设为0和1），而上式中$\hat{y_i}$通常不会在$(0,1)$的区间内，因此需要对网络的输出作处理。常用的方法是将$\hat{y_i}$作为某些函数的输入，该函数只要保证能够输出$(0,1)$即可，这里采用Sigmoid函数，定义为：

$$\sigma(x) = \frac{1}{1+e^{-x}}$$

1.2 Loss Function定义

Loss Function即反映网络对于样本的标签的估计值与实际标签之间的区别。Logistics回归期望当$y_i = 1$时$\hat{y_i} \approx 1$,而当$y_i = 0$时$\hat{y_i} \approx 0$.这里的$\hat{y_i}$其实可以看为概率。

常用的Loss Function：

$$y = \frac{1}{2}(\hat{y_i} - y_i)^2$$

但是由于Logistics回归的标签为0或1而非连续的，且对误差直接进行平方处理会导致后续无法用梯度下降法进行问题的求解（该曲线为非凸的）。

定义如下Loss Function：

$$L(\hat{y_i},y_i) = -((1-y)log(1-\hat{y_i}) + y log(\hat{y_i}))$$

Cost Function

Loss Function反映的是网络对单个样本的标签估计的准确程度，而Cost Function则是反映网络对于整个样本集（训练集）的准确程度。

神经网络（Neutral Network）

• 监督学习：样本输入->数据预处理->特征提取与选择->正向传播与计算损失函数->反向传播与更新网络参数与权重

强化学习（Reinforcement Learning）

Chapter 1 概述

  强化学习（Reinforcement Learning, RL）是一种试图让智能体在未知的不确定环境中通过最大化其获得的奖励来完成某些特定任务的算法。RL由智能体和环境两部分组成，在训练过程中Agent不断与环境（Environment）进行交互，在当前状态下自主输出一个Action(也叫Decision),这个Action输出到Agent中进被执行，从而获得下一个状态以及对应的Action所获得的奖励。Agent的目的就是尽可能多地从Environment中获得Reward。

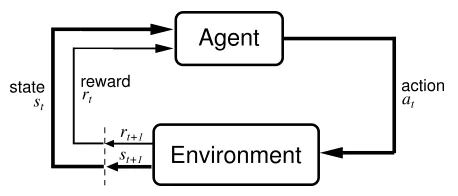
• 与监督学习相比，强化学习具有奖励反馈不及时地特点（延迟奖励），这会使得网络训练困难。
• 强化学习处理的大多数是序列数据，数据间不满足独立同分布。
• 需要不停地经过”试错“(trial-and-error exploration)来”学会”最有利的Action。
• 学习过程中没有很强的监督者，只有延迟性的奖励信号，没有即时反馈。
• 监督学习是在”专家”的指导下进行，因而算法的上限就是人类的表现，而RL则是在环境中自主探索，可以获得超越人类的能力。

①Reward: 环境反馈给Agent的标量信号(Scalar signal)。

②轨迹：当前帧以及Agent所采取的Action，即状态和动作的序列：

$$\tau = (s_0, a_0, s_1, a_1,...)$$

 可以通过观测序列和最终奖励来训练Agent，使其尽可能采取可以获得最终奖励的动作。一场”游戏”称为一个回合(Episode)或试验(Trial)。

③历史: 观测、动作、奖励的序列。

$$H_t = o_1, a_1, r_1 , ..., o_t, a_t, r_t$$

 由于Agent会根据历史决定当前的Action,因此可以把整个游戏的状态看作历史的函数：

$$s_t = f(H_t)$$

④状态一般是指环境的状态，而观测才是Agent的状态（因为Agent的状态并非完全可观测）。若完全可观测，则可当作一个马尔可夫决策过程(Markov Decision Process, MDP),这种情况下有$o_t = s_t^e = s_t^a$; 而当Agent只有部分状态可观测，则可作为部分可观测马尔可夫决策过程(Partiallly Observation Markov Decision Process, POMDP)。

  POMDP可以用一个七元组来描述：$(S, A, T, R, \Omega, O, \gamma)$, 其中$S$为状态空间，$A$为动作空间，$T(s^\prime|s,a)$为状态转移概率，$R$为奖励函数，$\Omega(o|s,a)$为观测概率，$O$为观测空间，$\gamma$为折扣因子。

⑤Action Space: 有效动作的集合，分为连续动作空间(动作是实值的向量)和离散动作空间(动作数量有限)。

⑥Pilocy: Agent按照Policy来选取Action，可分为随机性和确定性, RL中一般使用前者。前者为$\pi$函数，即$\pi(a|s) = p(a_t = a|s_t = s)$, 输入一个状态$s$，输出的是Agent采取的所有动作的概率，对这个概率进行采样即可得到Agent下一步的Action；后者则是直接采取最有可能的动作，即$a^* = \arg\max \limits_{a}\pi(a|s)$。
  注：$\arg\max \limits_{a}f(a)$ 指$f(a)$取得最大值时$a$的值。

⑦价值函数：对未来奖励的预测函数，用来评估状态的好坏。定义如下：

$$V_{\pi}(s) = \mathbb{E}_{\pi}[G_t|s_t = s] = \mathbb{E}_{\pi}[\sum_{k=0}^\infty \gamma^k r_{t+k+1}|s_t = s],对于所有的s \in S$$

 其中，期望$\mathbb{E}_{\pi}$的下标是$\pi$函数，$\pi$函数的值可以反映使用策略$\pi$时的奖励值。

 动作价值函数：Q函数，定义如下：

$$Q_{\pi}(s,a) = \mathbb{E}_{\pi}[G_t|s_t = s,a_t = a] = \mathbb{E}_{\pi}[\sum_{k=0}^\infty \gamma^k r_{t+k+1}|s_t = s,a_t = a]$$

易知：$V_{\pi}(s) = \sum\limits_{a \in A}\pi(a|s)Q_{\pi}(s,a)$

⑧模型：模型决定了下一步的状态。下一步的状态取决于当前的State和当前采取的Action，由状态转移概率和奖励函数两部分组成。前者定义为：

$$p_{ss^\prime}^a = p(s_{t+1} = s^\prime|s_t = s, a_t = a)$$

 后者指当前状态采取了某个动作所获得的奖励值，定义为：

$$R(s,a) = \mathbb{E}[r_{t+1}|s_t = s, a_t = a]$$

⑧基于策略的强化学习(Policy-based RL): 直接学习策略，输入一个状态，即可得到对应动作的概率。学习后，对于每一个状态，Agent都将会有一个与之对应的最佳动作。如：策略梯度算法。

 基于价值的强化学习(Value-based RL): 利用价值函数为导向，每个状态对应一个价值。显式地学习价值函数，隐式地学习策略，策略是通过价值函数推算得到的。维护一个价值表格或价值函数，通过这个表格或函数来选取价值最大的Action。只能应用于离散环境。如：Q-learning, Sarsa等。

 将以上两种RL结合起来就是Actor-Critic Agent(AC)。Agent根据策略做出动作，价值函数对所作出的动作给出价值，从而在原有的策略梯度算法的基础上加速学习过程。

⑨有模型RL: 需要对环境进行建模，构建一个虚拟环境来模拟真实环境中的交互。根据环境中的经验，构建虚拟世界，同时在真实环境和虚拟环境中进行学习。要求$(S, A, P, R)$均已知且$S$和$A$在有限步数内是有限集。（$P$即状态转移函数$p(s_{t+1}|s_t, a_t)$, $R$即奖励函数$R(s_t, a_t)$）

 免模型RL: 不对环境进行建模，直接与真实环境进行交互来学习最优策略，通常属于数据驱动方法，需要大量的采样来估计状态、动作及奖励函数，进而优化动作策略。

Chapter 2 MDP

2.1 Markov相关

• Markov property: 指一个随机过程在给定现在状态及所有过去状态情况下，其未来的状态的条件概率分布仅依赖于当前状态。也可描述为给定当前状态时，未来的状态与过去状态是条件独立的。
• Markov Process/Markov Chain: 马尔可夫过程是一组具有马尔可夫性质的随机变量序列$s_1, …, s_t$, 其中下一个状态只与当前的状态$s_t$有关。 $$p(s_{t+1}|s_t) = p(s_{t+1}|h_t)$$

  上式表明，从当前状态$s_t$转移到$s_{t+1}$，就等于其历史转移到$s_{t+1}$.
  离散时间的马尔可夫过程也被称为马尔可夫链。

2.1.1 Markov reward process

• MRP是MP加上奖励函数。其中奖励函数$R$是一个期望，表示当前当智能体达到某一个状态时可以获得多大的奖励。如果状态有限，则$R$可以是一个向量。

• (折扣)回报的定义：

$$G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \gamma^3 r_{t+4} + ... + + \gamma^{T-t-1} r_{t+t}$$

  折扣因子$\gamma$反映了我们对未来奖励的关注程度，当为0时说明我们只关注当前的奖励。折扣因子可作为智能体的一个超参(hyperparameter)来调整

• 对于MP，状态价值函数(State-value function)被定义为回报的期望：

$$\begin{equation} \begin{split} V^t(s) &= \mathbb{E}[G_t|s_t = s] \\ &= \mathbb{E}[r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ... + + \gamma^{T-t-1} r_{t+t}|s_t = s] \end{split} \end{equation}$$

2.1.2 价值函数

  当计算得到一些轨迹的实际回报时，价值函数可以通过这些轨迹的回报的平均值来得到，这种方法也就是通过蒙特卡洛(Mante Carlo, MC)采样的方法来计算价值。

• 贝尔曼方程（价值解析解）

  • 定义

    $$V(s) = R(S) + \gamma \sum_{s^\prime \in S}p(s^\prime|s)V(s^\prime)$$

     其中第一部分为即时奖励，第二部分则为未来奖励的折扣总和。

    • 全期望公式： $$\mathbb{E}[X] = \sum_i\mathbb{E}[X|A_i]p(A_i)$$
    • 条件期望: $$\mathbb{E}[X|Y = y] = \sum_xxp(X=x|Y=y)$$

  • 推导过程：

    $$\begin{equation} \begin{split} V(s) &= \mathbb{E}[G_t|s_t = s] \\ &= \mathbb{E}[r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ... + + \gamma^{T-t-1} r_{t+t}|s_t = s] \\ &= \mathbb{E}[r_{t+1}|s_t = s]+\gamma\mathbb{E}[r_{t+2} + \gamma r_{t+3} + ... + + \gamma^{T-t-2} r_{t+t}|s_t = s] \\ &= R(s) + \gamma\mathbb{E}[G_{t+2}|s_t = s] \\ &= R(s) + \gamma\mathbb{E}[V(s_{t+1})|s_t = s] \\ &= R(s) + \gamma\sum_{s^\prime \in S}p(s^\prime|s)V(s^\prime) \end{split} \end{equation}$$

  • 矩阵形式：$V = R + \gamma PV$
    解析解为：$V = (1-\gamma P)^{-1}R$

• 价值迭代法

  • 动态规划
    通过自举(bootstrapping)的方法对贝尔曼方程进行迭代直至收敛，即可得到某个状态的价值。

    对所有的状态$s \in S, V^\prime \leftarrow0,V(s)\leftarrow \infty$
    do
    $\quad$ $\quad$ $V\leftarrow V^\prime$
    $\quad$ $\quad$ 对于所有状态 $s\in S, V^\prime(s) = R(s) + \gamma \sum_{s^\prime \in S}P(s^\prime|s)V(s^\prime)$
    while ||$V - V^\prime$|| > $\epsilon$
    返回$V^\prime(s)$对于所有的状态$s\in S$

  • 蒙特卡洛
    从某个状态开始，随机产生若干条轨迹，计算每条轨迹对应的奖励，将每条轨迹的折扣奖励即回报进行累积$G_t$, 最后除以轨迹数量即可得到某个状态的价值。

    $i \leftarrow 0,G_t \leftarrow 0$
    while $i \neq N$,
    $\quad$ $\quad$生成一个回合的轨迹，从状态$s$和时刻$t$开始
    $\quad$ $\quad$使用生成的轨迹计算回报$g = \sum_{i=t}^{H-1}\gamma ^{i-t}r_i$
    $\quad$ $\quad$$G_t \leftarrow G_t + g, i \leftarrow i+1$
    $V_t \leftarrow G_t/N$

  • 时序差分学习(Temporal-difference learning, TD learning)

2.1.3 MDP

相对MRP，MDP多了决策（指动作），其定义类似，但状态转移多了一个条件：

$$p(s_{t+1}|s_t, a_t) = p(s_{t+1}|h_t, a_t)$$

• 策略
  定义了某个状态应该采取的动作。当知道当前状态后，带入策略函数$\pi$得到概率，这里的概率代表在当前的状态下可能采取的行动。策略也可能是确定性的，直接输出一个值，或者直接输出所要采取的行动。 $$\pi(a|s) = p(a_t = a|s_t = s)$$

• MDP到MRP的转换

  • 当知道了MDP以及$\pi$策略，通过以下式子即可实现转移： $$p_\pi(s^\prime|s) = \sum_{a \in A}\pi(a|s)p(s^\prime|s,a)$$
  • 奖励函数： $$R_{\pi}(s) = \sum_{a\in A}\pi(a|s)R(s,a)$$

  专业词汇（specialized vocabulary）

1. Step, Epoch, Batch, Episode, Iteration

• Step/Iteration: 整个样本集分的批次数
• Batch_size: 每个Step更新模型参数前所要学习的样本数
• Episode: 每个Episode会对模型进行一次验证，并保存最优的模型
• Epoch: 跑完整个训练集

  举例说明：一共有1000个训练样本，分为100批进行学习，即Step = 100, 则Batch_size = 1000/100 = 10. 因而1个Epoch包括了100个Iteration/若干个Episode,而一个Episode则包括了若干个Iteration.
  大小关系：Epoch > Episode > Iteration/Step

1. Policy: Agent的行为、策略，是state到action的映射，分为确定性(Deterministic)和随机性(Stochastic)。