Notes on RL Course of Hung-yi Lee
Outline
Lecture 1
Lecture 2
Lecture 3
Lecture 4
Lecture 5
Lecture 6
Lecture 7
Outline
Lecture 1
Lecture 2
Lecture 3
Lecture 4
Lecture 5
Lecture 6
Lecture 7
Appendix 1
Lecture 1
强化学习的基本思想是通过Agent与环境的不断交互,通过一些奖赏机制来使Agent逐渐学习出一条最优的决策。Agent在Environment中进行交互,由于Agent采取不同的Action会对Environment的State(对应到Agent的Observation)产生不同的影响,因而Environment会相应地返回不同的Reward,而RL的目标就是最大化最后的reward。
当环境的State完全可测时,则该问题可以被建模为马尔可夫决策过程(Markov Decision Process, MDP),此时State就等同于Observation。但事实上环境的State通常是部分可测的,因而也衍生了部分可观测马尔可夫决策过程(Partial Observable Markov Decision Process, POMDP)。
State是环境的状态,而Observation才是Agent的状态。

- 难点
- 延迟性的Reward
- Agent的Action会影响Environment
- 探索
- 利用
- RL通常分为Value-based和Policy-based两种,二者结合则是Actor-Critic(AC)。
- Value-based对应的是Critic, 而Policy-based则是Actor.
Asynchronous Advantage Actor-critic(A3C)
Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy P. Lillicrap, Tim Harley, David Silver Koray Kavukcuoglu, “Asynchronous Methods for Deep Reinforcement Learning”, ICML, 2016. Policy-based Approach(Actor is the policy)
- Action = $\pi$(Observation)
DRL三步走
- 决定网络的形式:Neural Network
- Input of NN: Observation
- Output of NN: 每个Action的概率(但不会直接选概率最大的Action)
决定评判标准: 整个episode的Reward(类似分类问题中的Loss)
- 让Actor $\pi_\theta (s)$进行一个Episode,其中$\theta$为网路的参数,$s$则是state, 在$s_i$时采取$a_i$会获得奖励 $r_i$, 则整个Episode的Reward为:$R_\theta = \sum_{i=1}^T r_i$.
- 由于采用随机性策略,加之环境的随性因素,对于相同的Actor,$R_\theta$都是不尽相同的.
- 目标不是使得某一个Episode的Reward最大,而是使得$\mathbb{E}(R_\theta)$最大.
因此,衡量标准就是$\mathbb{E}(R_\theta)$.
$\mathbb{E}(R_\theta)$的计算方法
- An episode is considered as a trajectory $\tau$
$\tau = \{s_1, a_1, r_1, s_2, a_2, r_2, …, s_T, a_T, r_T\}$
$R(\tau) = \sum\limits^{N}\limits_{n=1}r_n$ - 由于随机性,每个$\tau$都对应一个概率$P(\tau|\theta)$,因而可得:其中$\{\tau^1, \tau^2,…, \tau^N\}$为多条trajectory.
- An episode is considered as a trajectory $\tau$
更新参数$\theta$: Gradient Ascent 梯度上升
- $\theta^* = \argmax\limits_{\theta}\bar{R}_\theta$ s.t. $\bar{R}_\theta = \sum\limits_{\tau} R(\tau)P(\tau|\theta)$
Gradient ascent:
- start with $\theta^0$
- $\theta^{new} \leftarrow \theta^{old}+\eta\nabla\bar{R}_{\theta^{old}}$
- $\nabla\bar{R}_\theta$的计算方法
- $\nabla logP(\tau|\theta)$的计算:因而可得:
- 最终得到
Tricks 1: Add a Baseline
上述推导中,可以得到:$\nabla\bar{R}_\theta \approx \frac{1}{N}\sum\limits_{n=1}\limits^{N}\sum\limits_{t=1}\limits^{T_n}R(\tau^n)\nabla logp(a_t^n|s_t^n,\theta)$.
上式的目的其实就是提高能够使Reward增加的Action的概率增大,而为负的则会减少,且对于Reward贡献大的Action增加的概率相比贡献少的提升率要高(可以把Reward的值当作分类问题中的权重,假设某个Trajectory的Reward为2,那么上式就相当于把这条Trajectory复制两遍,从而更好地提高该Trajectory的概率)。但实际上可能出现某个Action可以使得最后的Reward变大,然而并没有被Sample到,而其他Action也可以使Reward增加,但是增加率不高,根据上式,这些“不是很好的”Action的概率将被提高,而对于没被Sample到的“好”Action概率却被降低了。因此,为避免上面所述的情况,更改上式为:
即增加一个Baseline作为标准,“不是很好的”Action的贡献低于Baseline,那么这些Action的概率就会被降低,从而间接地提高了没被Sample到地“好”Action的概率。
Baseline的设计方法通常是:$b \approx \mathbb{E}[R(\tau)]$.
- Trick 2:Assign Suitable Credit
- 根据推导出来的公式,对于某一个Trajectory $\tau^i$,其中每个Action的权重都是那个Trajectory的Reward(即$R[\tau^i]$), 但并不是$\tau^i$中的每个$a^i_t$都是利于增加$R[\tau^i]$. 因此,对不同的Action给予不同的权重Weight更为合理。
- 实现方式:修改上式为
加入discount factor(好像变成了MDP了)
- 然后将以上式子中的$(\sum\limits_{t^{\prime}=t}\limits^{T_n}\gamma ^{t^\prime-t}r^n_{t^\prime}-b)$用一个Advantage Function $A^\theta(s_t, a_t)$来代替.(由Critic评估),则变成:
- 决定网络的形式:Neural Network
- Value-based Approach(Critic)
- Value-based的方法并不直接决定Agent的Action,而是给出Actor $\pi$在状态$s_t$时的评价,即给出$V^\pi(s)$
- Mante-Carlo(对整个Episode)
- Temporal Difference(对每一步)
- 给出Actor $\pi$在状态$s_t$采取$a_t$时的评价$Q^\pi(s, a)$

Actor + Critic: 由于环境具有随机性,AC算法让Agent不再跟环境反馈的奖励进行学习,而是跟着Critic学习
Policy Gradient属于on-policy的方法,而Proximal Policy Optimization(PPO)则是PG的变型,属于off-policy方法,并加上某些约束。
- on-policy: 训练的Agent和与环境互动的Agent是同一个(一边互动一边学习)。
off-policy:训练的Agent和与环境互动的Agent不是同一个。
- PG中每次Sample的数据都只用一次,更新完参数$\theta$后需要Sample新的数据进行训练。
Importance Sampling:
注意:p(x)和q(x)区别不能过大,否则采样不准确。
如果p(x)和q(x)区别过大,则$Var_{x\sim p}[f(x)]$和$Var_{x\sim q}[f(x)]$不对等,导致采样失真。
- 应用Importance Sampling,可以将期望奖励的梯度做如下转换:
从而实现在$\theta^\prime$下采集数据喂给$\theta$,即实现on-policy到off-policy的转换。
- 加上L1中提到的Trick后,则变成:
从而得到新的Objective Function为:$J^{\theta^\prime}(\theta) = E_{(s_t,a_t)\sim \pi_{\theta^\prime}}[\frac{p_\theta(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)}A^{\theta^\prime}(s_t, a_t)]$
- PG中每次Sample的数据都只用一次,更新完参数$\theta$后需要Sample新的数据进行训练。
PPO:
- PPO2:
其中,$clip()$定义为: - TRPO:
这里的KL距离并不是指参数上的距离,而是其行为上的区别。,即喂同样的State,输出的Action类似。
Lecture 3
- Q-learning是一种Value-based的方法,不直接决定Action,只评估Actor的好坏。
- 状态价值函数: $V^\pi(s)$, 在某个状态$s$时给出Actor $\pi$的Reward(可以看作获得奖励的潜力). $V^\pi(s)$的值取决于Actor本身以及环境的状态$s$.
- 评价方法:
- Monte-Carlo based approach: 需要跑完整个trajectory才更新一次参数
$V^\pi(s_a) = G_a$
$V^\pi(s_b) = G_b$
… - Temporal-difference(TD) approach
$V^\pi(s_t) - V^\pi(s_{t+1}) \rightarrow r_t$
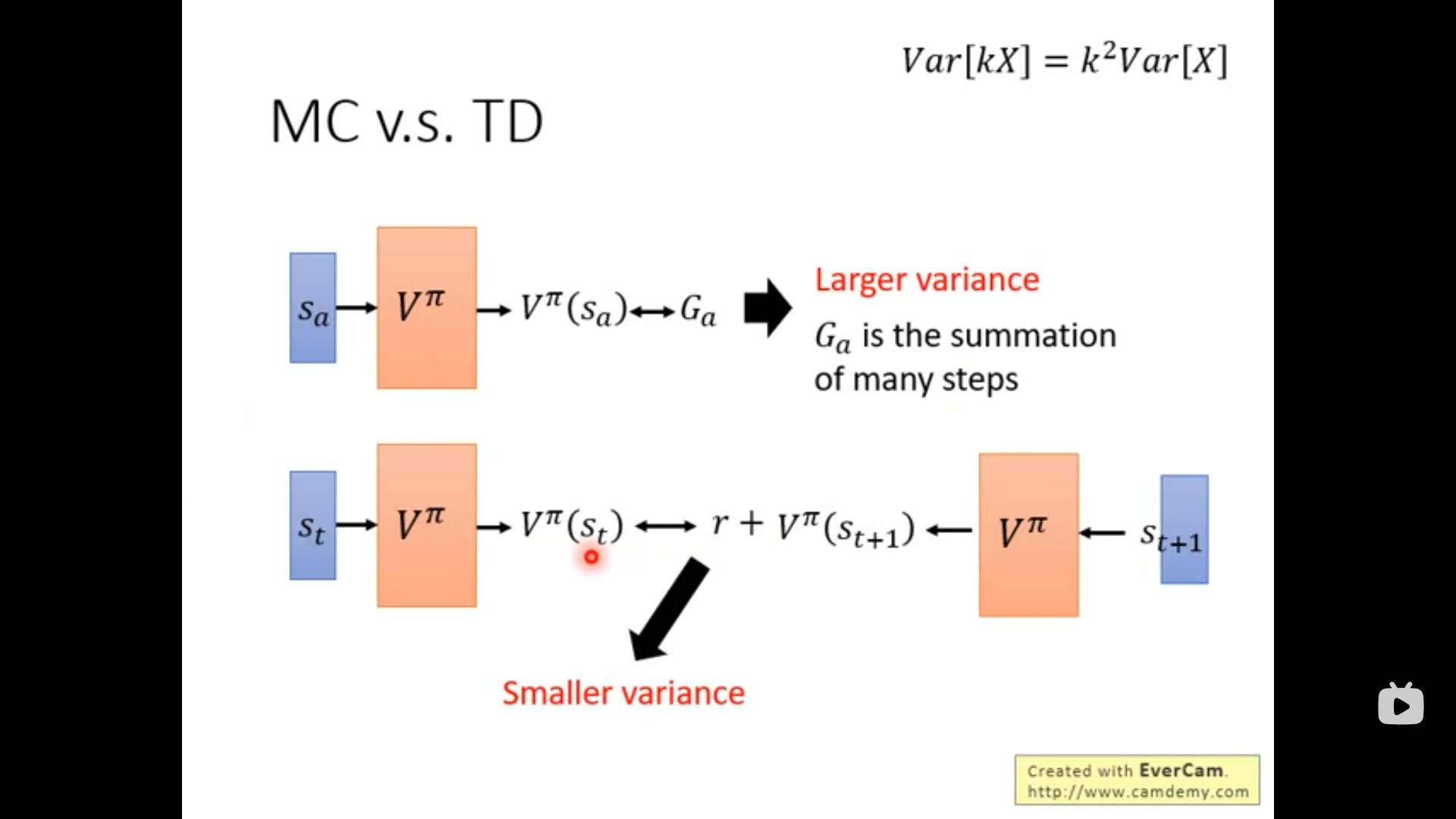
- Monte-Carlo based approach: 需要跑完整个trajectory才更新一次参数
- 评价方法:
- 状态行为价值函数:$Q^\pi(s,a)$, 在某个状态$s$下强制采取动作$a$带来的Reward(但实际并不一定采取该行为,即这个Reward是preditive),这种方法由于需要穷举每个可能的Action,所以只适合具有有限个Action的情况.
- Trick 1: 固定$Q^\pi(s_{t+1},a_{t+1})$的Q-Table,只更新$Q^\pi(s_{t},a_{t})$的Q-Table,经过若干个Step再将后者复制到前者中。
- Trick 2: 加入Exploration机制
- Epsilon Greedy:当(random() < $\epsilon$时采取随机Action,当random()>1-$\epsilon$时采取$\arg \max\limits_{a} Q(s,a)$).($\epsilon$随学习的进行而减小).
- Boltzmann Exploration: $P(a|s) = \frac{\exp{Q(s,a)}}{\sum\limits_{a}{\exp{Q(s,a)}}}$(相当于把Q-Table某一行的每一个Action对应的Value进行归一化,然后按照归一化后的数值作为概率选择Action)
- Trick 3: 创建一个缓冲区,存放过往的数据,每次都从缓冲区随机取若干个数据进行学习,并将新的数据存进缓冲区(因而缓冲区的数据可能来自不同的policy),当缓冲区满了才将旧数据丢弃。
采用Trick3,实际上变成了off-policy-like方法.
- Q-learning的实质:使得$Q^\pi(s_t,a_t)$和$Q^\pi(s_{t+1},a_{t+1})$的差变小。

DQN的一些改进版本
Double DQN
- 解决DQN中的Q-value被高估的问题
- 神经网络的估计误差的存在会导致某些Action的Q-value被高估,而DQN中会选择Q-value中最大值加上Reward来作为Target,从而使得原本的Q-value接近于Target,进而导致被“高估”的动作的Q-value越来越大。
- Double DQN的解决办法: 用一个Q-network选择价值最高的Action,而Action的Q-value由另一个Q-network来评估。即:
- 实现:用DQN中待更新的Q-network来选Action,用Target Q-network来评估Q-value.
Dueling DQN
- 更改了DQN的架构:两个输出,一个为$V(s)$, 另一个为$A(s,a)$, 二者的加和为Q-value, 即$Q(s,a) = A(s,a) + V(s)$
- 好处:即使某个A-S没被Sample到,其对应的Q-value可以通过修改V(s)来修改,即不需要所有的动作-状态对都被采样,提高数据的利用效率。
- 由于希望Network尽可能地修改$V(s)$而不是修改$A(s,a)$,可以添加一个约束:即$A(s,a)$每一列的加和为0
- 实现方法:将Q-network的输出中的$A(s,a)$先进行处理,使其列的加和为0,再进行输出的合并得到Q-table。
- Noisy Net: 在每个Episode开始前对Q-network的参数加上Gaussian noise
- 与$\epsilon$-greedy的区别:Noisy Net是直接在参数上加noise,但最后对于相同(相似)的State,采取的动作都会是最优的,其探索是与状态有关的,即State-dependent Exploration;而后者则是在Action上加noise,即对于同样的State,Actor采取的动作可能是不同的,因而这种的做法的探索都是随机的。
- Distributional Q-function:原本的DQN的输出的Q-value的期望,而这种方法则是输出其分布
- 应用:不同的分布可能具有相同的期望值,但是其方差不同,方差较大者风险也较大,因而可以加入一个网络来进行风险的规避.
- 对于动作空间是连续性,可以采用:①对动作空间进行采样,但这种办法会降低精确度;②通过梯度上升法来解决最优问题;③人为设计Q-function.

Lecture 4
Advantage Actor-Critic(A2C)
- Tips
- Actor和Critic共享参数

- Actor和Critic共享参数
- Tips
Asynchronous Advantage Actor-Critic(A3C)

Lecture 5
Model-free和Model-based的区别
Model-based: 概率函数(Probability function)和奖励函数(Reward Function)均已知(值迭代和策略迭代都是Model-based的方法,二者均需要得到环境的转移和奖励函数,迭代过程中不需要和环境进行交互)概率函数实际上是反映环境的随机性。
Model-free: 采用V函数来评价当前状态的好坏,使用Q函数来判断某个状态下某一动作的好坏,通过交互、试错的方法进行环境的探索和策略的优化。Model-free没有获取环境的状态转移和奖励函数,我们让 agent 跟环境进行交互,采集到很多的轨迹数据,agent 从轨迹中获取信息来改进策略,从而获得更多的奖励。
Model-free Prediciton
Monte-Carlo Policy Evaluation
- 采用策略$\pi$计算折扣奖励Return:$G_t = R_{t+1} + \gamma R_{t+2}+ \gamma^2 R_{t+3} + …$
- Sample足够多的Trajectory,循环计算每条Trajectory对应的折扣奖励,最后进行平均得到价值函数$V^\pi(s)$
MC采取经验平均回报(Empirial mean return)的方式来估计价值函数;只能应用在有限回合的MDP问题(Episodic MDPs)
- 增量MC
- MC算法如下:
估计V(s)
$N(s)\leftarrow N(s) + 1$
$S(S)\Leftarrow S(s) + G_t$
$v(s) = S(s)/N(s)$
根据大数定律,当$N(s)\rightarrow \infty$时,有$V(s)\rightarrow V^\pi(s)$ - 增量MC:
估计V(s)
$N(S_t)\leftarrow N(S_t) + 1$
$V(S_t)\Leftarrow V(s) + \frac{1}{N(S_t)}(G_t - V(S_t))$
将$\frac{1}{N(S_t)}$视为学习率,则
- MC算法如下:
- MC和DP的区别:前者是通过上一时刻的下一状态的价值函数来更新当前时刻当前状态的价值函数,即用$V_{i-1}(s^\prime)$来更新$V_{i}(s)$(其中i为迭代次数);后者则是通过empirical mean return (实际得到的收益)来更新,采用的是实际发生的Trajectory,并且只更新与这条Trajectory有关的状态(直接通过轨迹来更新,其实已经暗含了环境的随机性,只要轨迹的数量足够多,Agent仍然可以学会环境的随机性)
Temporal Difference(TD) learning
- 对于某个给定的策略,在线(online)地算出它的价值函数,每往前若干步就更新上一时刻的V值
- TD(0):
$V(s_t)\leftarrow v(s_t) + \alpha\big(R_{t+1}+\gamma v(s_{t+1}) - v(s_t)\big)$
- n步TD:
$G_t^n = R_{t+1} + \gamma R_{t+2} + … + \gamma^{n-1} R_{t+n}+\gamma^n v(S_{t+n})$
$v(S_t) \leftarrow v(S_t) + \alpha(G^n_t - v(S_t))$
- TD(0):
- 对于某个给定的策略,在线(online)地算出它的价值函数,每往前若干步就更新上一时刻的V值
Model-free control
- Model-based Policy Iteration: 对以下两个式子进行迭代直至收敛
- Model-free中$R(s,a)$和$P(s^\prime|s,a)$均未知,因而采用MC的方法估计Q函数,然后同样采用贪心的想法更新改进策略。
- Model-based Policy Iteration: 对以下两个式子进行迭代直至收敛
Sarsa: 同策略时序差分控制
将时序差分法更新V值的过程,更改为更新Q,即:对于一条轨迹而言,Q值就等同于V值,且有:$Q(s_t,a_t) = r + \gamma Q(s_{t+1},a_{t+1})$
n步Sarsa
- 更新方式:
n = 1(Sarsa) $q_t^{(1)} = R_{t+1}+\gamma Q(S_{t+1}, A_{t+1})$
n = 2 $q_t^{(2)} = R_{t+1}+\gamma R_{t+2} + \gamma^2Q(S_{t+2}, A_{t+2})$
…
n = $\infty$(MC) $q_t^\infty = R_{t+1}+\gamma R_{t+2} + … + \gamma^{T-t-1}R_T$
- 更新方式:
Sarsa($\lambda$)

