Markov Decision Process
简介
马尔可夫链:状态$s_{t+1}$只与上一个状态有关,而与其他历史无关,即
- $p(s_{t+1}|s_t) = p(s_{t+1}|h_t)$
- $p(s_{t+1}|s_t, a_t) = p(s_{t+1}|h_t, a_t)$
Markov Reward Process(MRP)
- 在马尔可夫链的基础上加入了Reward
- 状态集有限
- Reward: $R(s_t) = \mathbb{E}[r_t|s_t = s]$
- Transition probabilit: $p(s^\prime|s)$
- 折扣因子:$\gamma$
- 状态价值函数:其中$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} +… + + \gamma^{T-t-1} R_{T}$为折扣奖励。
计算实例
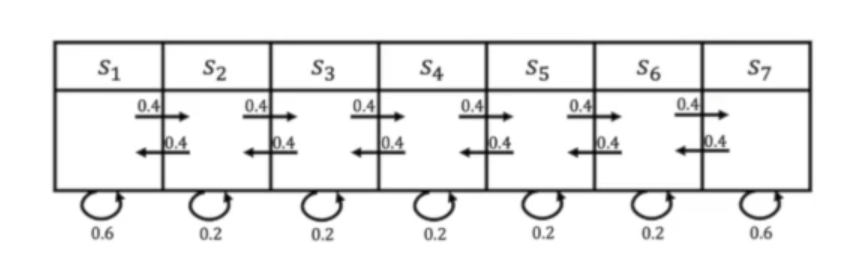
Reward: R = [5, 0 ,0, 0, 0, 0, 10]
Trajectory as: $\tau_1 = [s_4, s_5, s_6, s_7]$, $\tau_2 = [s_4, s_3, s_2, s_1]$, $\tau_3 = [s_4, s_5, s_6, s_6]$
if $\gamma$ set as $\gamma = 0.5$, then $R(\tau_i)$ can be calculated:
$R(\tau_1) = 0 + 0.50 + 0.5^20 + 0.5^310 = 1.25$
$R(\tau_2) = 0 + 0.50 + 0.5^20 + 0.5^35 = 0.625$
$R(\tau_3) = 0 + 0.50 + 0.5^20 + 0.5^3*0 = 0$
Value of state $s_4$:①$V(s_4) \approx \frac{1}{N}\sum\limits_{i = 1}\limits^{N}R(\tau_i)$
②Bellman equation : $V(s) = R(s) + \gamma \sum\limits_{s^\prime \in S}P(s^\prime|s)V(s^\prime)$
$V = (I - \gamma P)^{-1}R$
- 状态价值函数计算
- Monte-Carlo方法
随机产生多条轨迹,然后求平均:$V(s) \approx \frac{1}{N}\sum\limits_{i = 1}\limits^{N}R(\tau_i)$
- 动态规划(迭代)
$V(s) = R(s) + \gamma \sum\limits_{s^\prime \in S}P(s^\prime|s)V(s^\prime)$
- Temporal Difference
$V(s) = R_t + V(s^\prime)$
Markov Decision Process(MDP)
- 在MRP的基础上加上决策(即加上动作)
- 状态集有限
- 动作集有限
- Transition Probability: $p(s_{t+1}|s_t, a_t)$
- Reward: $R(s_t, a_t) = \mathbb{E}[r_t|s_t, a_t]$
- Policy of MDP
- 分为确定性和随机性两种,前者输出动作,后者输出每个动作对应的概率
- 状态动作价值函数
MDP与MRP的转换
- 在$\pi$已知的前提下
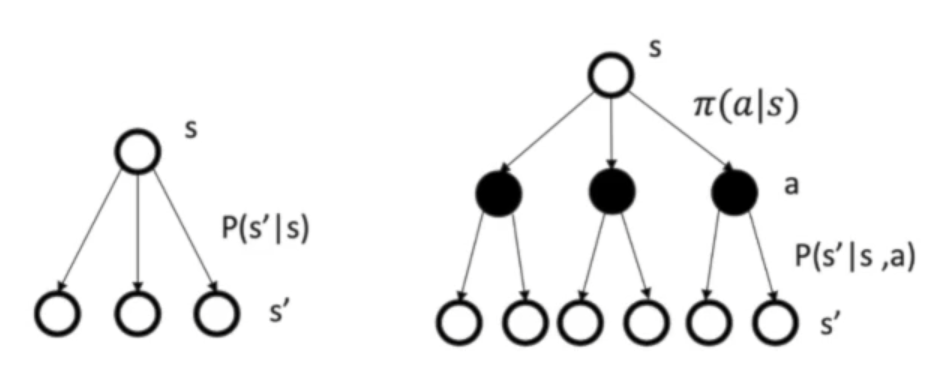
MDP的预测与控制
- 预测:输入为MDP<$S,A,P,R,\gamma$>和$\pi$或MRP<$S,P^\pi,R^\pi, \gamma$>, 输出为价值函数$V^\pi$
- 控制:输入为MDP<$S,A,P,R,\gamma$>,输出为最优价值函数$V^$和最佳策略$\pi^$
简介
马尔可夫链:状态$s_{t+1}$只与上一个状态有关,而与其他历史无关,即
- $p(s_{t+1}|s_t) = p(s_{t+1}|h_t)$
- $p(s_{t+1}|s_t, a_t) = p(s_{t+1}|h_t, a_t)$
Markov Reward Process(MRP)
- 在马尔可夫链的基础上加入了Reward
- 状态集有限
- Reward: $R(s_t) = \mathbb{E}[r_t|s_t = s]$
- Transition probabilit: $p(s^\prime|s)$
- 折扣因子:$\gamma$
- 状态价值函数:其中$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} +… + + \gamma^{T-t-1} R_{T}$为折扣奖励。
计算实例

Reward: R = [5, 0 ,0, 0, 0, 0, 10]
Trajectory as: $\tau_1 = [s_4, s_5, s_6, s_7]$, $\tau_2 = [s_4, s_3, s_2, s_1]$, $\tau_3 = [s_4, s_5, s_6, s_6]$
if $\gamma$ set as $\gamma = 0.5$, then $R(\tau_i)$ can be calculated:
$R(\tau_1) = 0 + 0.50 + 0.5^20 + 0.5^310 = 1.25$
$R(\tau_2) = 0 + 0.50 + 0.5^20 + 0.5^35 = 0.625$
$R(\tau_3) = 0 + 0.50 + 0.5^20 + 0.5^3*0 = 0$
Value of state $s_4$:①$V(s_4) \approx \frac{1}{N}\sum\limits_{i = 1}\limits^{N}R(\tau_i)$
②Bellman equation : $V(s) = R(s) + \gamma \sum\limits_{s^\prime \in S}P(s^\prime|s)V(s^\prime)$
$V = (I - \gamma P)^{-1}R$- 状态价值函数计算
- Monte-Carlo方法
随机产生多条轨迹,然后求平均:$V(s) \approx \frac{1}{N}\sum\limits_{i = 1}\limits^{N}R(\tau_i)$ - 动态规划(迭代)
$V(s) = R(s) + \gamma \sum\limits_{s^\prime \in S}P(s^\prime|s)V(s^\prime)$ - Temporal Difference
$V(s) = R_t + V(s^\prime)$
- Monte-Carlo方法
- 在马尔可夫链的基础上加入了Reward
Markov Decision Process(MDP)
- 在MRP的基础上加上决策(即加上动作)
- 状态集有限
- 动作集有限
- Transition Probability: $p(s_{t+1}|s_t, a_t)$
- Reward: $R(s_t, a_t) = \mathbb{E}[r_t|s_t, a_t]$
- Policy of MDP
- 分为确定性和随机性两种,前者输出动作,后者输出每个动作对应的概率
- 状态动作价值函数
- 在MRP的基础上加上决策(即加上动作)
MDP与MRP的转换
- 在$\pi$已知的前提下

MDP的预测与控制
- 预测:输入为MDP<$S,A,P,R,\gamma$>和$\pi$或MRP<$S,P^\pi,R^\pi, \gamma$>, 输出为价值函数$V^\pi$
- 控制:输入为MDP<$S,A,P,R,\gamma$>,输出为最优价值函数$V^$和最佳策略$\pi^$
