字典树

概念

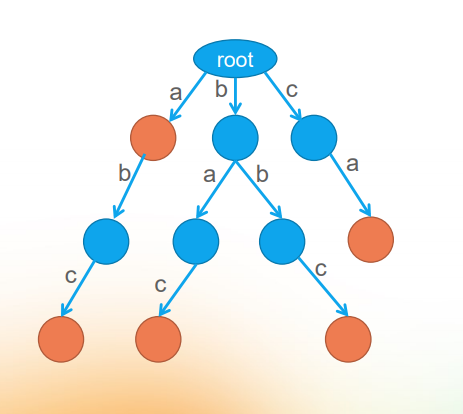
字典树是一种按照字符串的前缀构建的一种特殊数据结构，是一种字典的存储结构，每个“单词”从根节点出发一直到某一节点为止的路径（通过节点上的bool end来判断是否为单词结尾），路径上的字母连起来即是所存储的“单词”。

功能

维护字典树（即插入“单词”）
查询字典树中是否存在某一完整字符串
统计字符串出现次数
字典序排序
求集合内字符串之间的公共前缀

实现

设计

结构体定义

typedef struct Trie {
    bool end;               //用来记录从根节点到当前节点的路径是否为一个完整字符串
    struct Trie *next[26];  //普通字符串只有26种字符
} Trie;

创建节点

Trie* trieCreate() {
    struct Trie *node = (struct Trie *)malloc(sizeof(Trie));
    node->end = false;
    memset(node->next, 0, sizeof(node->next));
    return node;
}

c++中以上两个操作可以直接进行合并，定义一个Trie类，然后创建节点即为Trie类的构造函数.

插入操作

void trieInsert(Trie* obj, char * word) {
    int n = strlen(word);
    Trie *cur = obj;
    for(int i = 0; i < n; i++){
        int childptr = word[i] - 'a';           //将字符映射到整型
        if(cur->next[childptr] == NULL){        //为null说明字典树中没有该单词
            cur->next[childptr] = trieCreate();
        }
        cur = cur->next[childptr];
    }
    cur->end = 1;   //单词插入完成，将当前节点的end置true来表示为单词末尾
}

查询字典中是否存在某个完整字符串

bool trieSearch(Trie* obj, char * word) {
    int n = strlen(word);
    Trie *cur = obj;
    for(int i = 0; i < n; i++){
        int childptr = word[i] - 'a';
        if(cur->next[childptr] == NULL){    //为null说明当前的单词不存在于字典树中，返回false
            return false;
        }
        cur = cur->next[childptr];
    }
    return cur->end;    //如果字典树中存在路径与单词相重合，直接判断当前节点是否为true
}

查询字典中是否存在某个字符串前缀

bool trieStartsWith(Trie* obj, char * prefix) {
    int n = strlen(prefix);
    Trie *cur = obj;
    for(int i = 0; i < n; i++){
        int childptr = prefix[i] - 'a';
        if(cur->next[childptr] == NULL){
            return false;
        }
        cur = cur->next[childptr];
    }
    return true;    //与完整字符串不同的地方是不需要看当前节点是不是单词的末尾
}

应用

648. 单词替换

在英语中，我们有一个叫做词根(root) 的概念，可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为继承词(successor)。例如，词根an，跟随着单词other(其他)，可以形成新的单词another(另一个)。

现在，给定一个由许多词根组成的词典dictionary和一个用空格分隔单词形成的句子sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根，则用最短的词根替换它。

你需要输出替换之后的句子。

示例1:

输入：dictionary = [“cat”,”bat”,”rat”], sentence = “the cattle was rattled by the battery”
输出:”the cat was rat by the bat”

示例2:

输入*：dictionary = [“a”,”b”,”c”], sentence = “aadsfasf absbs bbab cadsfafs”
输出：”a a b c”
- 思路：将dictionary中的词根存入到一个字典树中，并在字典树中依次查找sentence的每个单词并返回对应的前缀，如果不存在相应的前缀则返回原来的单词，并将结果存在答案res中即可。

class Tries {
public:
    bool end;
    Tries *next[26];
    
    Tries(){
        end = false;
        memset(next, 0, sizeof(next));
    }

    void Insert(Tries *obj, string word){
        int n = word.length();
        Tries *cur = obj;
        for(int i = 0; i < n; i++){
            int childptr = word[i] - 'a';
            if(cur->next[childptr] == NULL){
                cur->next[childptr] = new(Tries);
            }
            cur = cur->next[childptr];
        }
        cur->end = true;
    }
    
    string findPredix(Tries *obj, const string& word){
        string Predix;
        Tries *cur = obj;
        for(char ch: word){
            int childptr = ch - 'a';
            if(cur->next[childptr] != NULL){
                if(cur->end == true)    break;
                Predix += ch;
            }else{
                break;
            }
            cur = cur->next[childptr];
        }
        return cur->end == true ? Predix : word;
    }
};

class Solution {
public:
    string replaceWords(vector<string>& dictionary, string sentence) {
        string res;
        Tries *root = new(Tries);
        for(string str: dictionary){
            root->Insert(root, str);
        }
        string tmpStr;
        for(int i = 0; i < sentence.length(); i++){
            char ch = sentence[i];
            if(ch != ' '){
                tmpStr += ch;
            }else{
                string str = root->findPredix(root, tmpStr);
                res += str + " ";
                tmpStr = "";
            }
        }
        res += root->findPredix(root, tmpStr);
        return res;
    }
};

1. 421. 数组中两个数的最大异或值
2. 剑指 Offer II 067. 最大的异或
  
  给定一个整数数组nums，返回nums[i] XOR nums[j]的最大运算结果，其中0 ≤ i ≤ j < n。
  
  示例1:
  
  输入:nums = [3,10,5,25,2,8]
  输出:28
  
  示例2:
  
  输入:nums = [0]
  输出:0
  
  示例3:
  
  输入:nums = [2,4]
  输出:6
  
  示例4:
  
  输入:nums = [8,10,2]
  输出:10
  
  示例5:
  
  输入:nums = [14,70,53,83,49,91,36,80,92,51,66,70]
  输出:127
  - 思路：将每个数转换为二进制字符串并按由高位到低位建立字典树(不能由低到高，因为字典树中树的左右子树的深度未知，需要遍历整个树才能得到答案，基本上就是$O(n^2)$的复杂度了；而由高到低，我们只需要按照有相反的路径就走相反的路径、没有就走相同的路径，尽可能往深的走，那么就一定能得到答案),然后对数组进行遍历，即可得到答案。这道题属于01字典树,经典题目。

class Tries {
public:
    Tries *next[2];
    Tries(){
        memset(next, 0, sizeof(next));
    }

    void insert(Tries *obj, string tmpStr){
        Tries *cur = obj;
        for(char ch: tmpStr){
            int childptr = ch - '0';
            if(cur->next[childptr] == NULL){
                cur->next[childptr] = new(Tries);
            }
            cur = cur->next[childptr];
        }
    }

    int search(Tries *obj, string tmpStr){
        Tries *cur = obj;
        int res = 0;
        for(char ch: tmpStr){
            //代码优化版，性能并没有优化
            /*int childptr = (ch - '0') ^ 1;  //取相反数，0取1，1取0
            if(cur->next[childptr]){
                res = 2*res + 1;
            }else{
                childptr ^= 1;
                res = 2*res;
            }
            cur = cur->next[childptr];*/
            int childptr = (ch - '0');
            if(childptr){               //当前位为1
                if(cur->next[0]){       //相反位不为null
                    cur = cur->next[0]; //则往相反位走
                    res = 2*res + 1;    //加上当前位1
                }else{  
                    cur = cur->next[1]; //相反位为null，走同位
                    res = 2*res;        //当前位相同，不加1
                }
            }else{                      //当前位为0
                if(cur->next[1]){       //相反位不为null
                    cur = cur->next[1]; //则往相反位走
                    res = 2*res + 1;    //加上当前位1
                }else{
                    cur = cur->next[0]; //相反位为null，走同位
                    res = 2*res;        //当前位相同，不加1
                }
            }
        }
        return res;
    }
};

class Solution {
public:
    int findMaximumXOR(vector<int>& nums) {
        Tries *root = new(Tries);
        int ans = 0;
        string s = "";
        for(int num: nums){ //构建01字典树
            for(int i = 30; i >= 0; --i){   //数转二进制字符串，题目中num<2^31-1,所以最多是30位
                s += ('0' + ((num>>i) & 1));
            }
            root->insert(root, s);          //插入字典树
            s = "";                         //清空中间字符串
        }
        for(int num: nums){
            for(int i = 30; i >= 0; --i){
                s += ('0' + ((num>>i) & 1));//数转二进制字符串
            }
            ans = max(ans, root->search(root, s));
            s = "";                         //清空中间字符串
        }
        return ans;
    }
};

Vyron Su

http://example.com/2022/04/03/Tries/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Vyron Su !

字典树

monotone stack

2022-04-04 刷题

Cpp 单调栈

Value Iteration vs Policy Iteration

2022-03-31 学习

Reinforcement Learning 值迭代策略迭代