leetcode-79/130/1091

Cpp 深度优先搜索广度优先搜索

刷题

发布日期: 2022-04-10

79. 单词搜索
- 思路
- 代码
- 优化
130. 被围绕的区域
- 思路
- 代码
1091. 二进制矩阵中的最短路径
- 思路
- 代码
总结

1 单词搜索

题目链接：79. 单词搜索

1.1 题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例1:

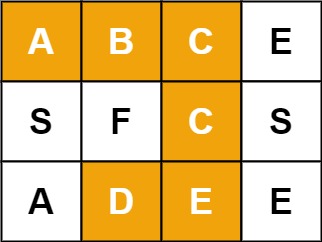
输入: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”
输出: true

示例2:

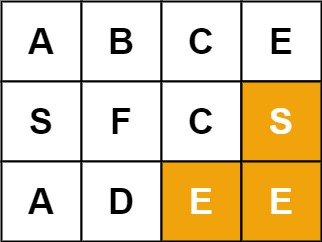
输入: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “SEE”
输出: true

示例3:

输入: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCB”
输出: false

1.2 思路

典型的深度优先搜索，按照对整个 board 进行遍历，由于题目中要求同一个单元格内的字母不允许被重复使用，因而需要创建一个 visited 矩阵来记录已经访问过的格子，避免“重蹈覆辙”。当当前所遍历到的位置的字符等于 word 的第一个字符时进行 dfs ，按照上、下、左、右四个方向进行搜索，返回条件有三个：①索引越界；② word 已经匹配完成；③当前搜索的位置与 word 当前位字符不同。即返回条件为：

if(pos==len||r<0||c<0||r>=m||c>=n||visited[r][c]||board[r][c]!=word[pos]) return;

需要注意的是：每次进行递归前要将当前格子的 visited 置位并将 word 指针后移一位，递归完成后都要将当前位置的 visited 进行清空，即回溯中的”撤回”操作，并判断 word 已经匹配完成，未完成则将 word 的指针减 1 , 这也是”撤回”。因而单层一个方向的递归应该为:

{
    visited[r][c] = true;
    pos++;
    dfs(board, word, r+1, c);
    if(pos==len) return;
    visited[r][c] = false;
    pos--;
}

四个方向的搜索则为：

{
    visited[r][c] = true;
    pos++;
    dfs(board, word, r+1, c);   //下
    if(pos==len) return;
    dfs(board, word, r-1, c);   //上
    if(pos==len) return;
    dfs(board, word, r, c+1);   //右
    if(pos==len) return;
    dfs(board, word, r, c-1);   //左
    if(pos==len) return;
    visited[r][c] = false;
    pos--;
}

完整代码如下：

class Solution {
public:
    int  m , n, len, pos;
    bool visited[6][6], check = false;

    void dfs(vector<vector<char>>& board, string word, int r, int c){
        if(pos==len||r<0||c<0||r>=m||c>=n||visited[r][c]||board[r][c]!=word[pos]){
            return;
        }else{
            visited[r][c] = true;
            pos++;
            dfs(board, word, r+1, c);
            if(pos==len) return;
            dfs(board, word, r-1, c);
            if(pos==len) return;
            dfs(board, word, r, c+1);
            if(pos==len) return;
            dfs(board, word, r, c-1);
            if(pos==len) return;
            visited[r][c] = false;
            pos--;
        }
    }

    bool exist(vector<vector<char>>& board, string word) {
        m = board.size(), n = board[0].size(), len = word.length();
        if(len > m*n){
            return false;
        }
        for(int r = 0; r < m; ++r){
            for(int c = 0; c < n; ++c){
                pos = 0;
                memset(visited, false, sizeof(visited));
                dfs(board, word, r, c);
                if(pos == len) return true;
            }
        }
        return false;
    }
};

1.3 改进

前边我们定义了一个 pos 指针用于表示 word 匹配的位置，返回条件为 pos 等于 word 的长度，那么每一次递归后回溯都需要进行这个条件的判断：if(pos==len) return; , 我们需要进行四个方向的递归，那么就需要判断四次(如果没有判断那么四层 dfs 完成后将会把 pos 减去1，当返回主函数是 pos 已经不再等于 word 的长度)，虽然逻辑表达上更为清晰，但会导致代码过于冗余，我们可以将 pos 作为一个 dfs 的一个参数，转而创建一个全局的 bool check ，一旦我们完成了匹配则将 check 置位并返回，而后不再需要对 pos 进行判断，每一层 dfs 只要检测到 check 为 true 则直接返回。

class Solution {
public:
    int  m , n, len;
    bool visited[6][6], check = false;

    void dfs(vector<vector<char>>& board, string word, int r, int c, int pos){
        if(check||r<0||c<0||r>=m||c>=n||visited[r][c]||board[r][c]!=word[pos]){
            return;
        }else{
            if(pos == len-1){
                check = true;
                return;
            }
            visited[r][c] = true;
            dfs(board, word, r+1, c, pos+1);
            dfs(board, word, r-1, c, pos+1);
            dfs(board, word, r, c+1, pos+1);
            dfs(board, word, r, c-1, pos+1);
            visited[r][c] = false;
        }
    }

    bool exist(vector<vector<char>>& board, string word) {
        m = board.size(), n = board[0].size(), len = word.length();
        if(len > m*n){
            return false;
        }
        for(int r = 0; r < m; ++r){
            for(int c = 0; c < n; ++c){
                memset(visited, false, sizeof(visited));
                dfs(board, word, r, c, 0);
                if(check) return true;
            }
        }
        return false;
    }
};

2 被围绕的区域

题目链接：130. 被围绕的区域

2.1 题目描述

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1:

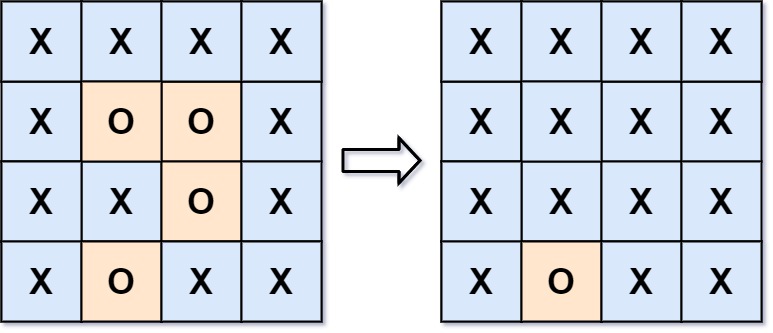
输入: board = [[“X”,”X”,”X”,”X”],[“X”,”O”,”O”,”X”],[“X”,”X”,”O”,”X”],[“X”,”O”,”X”,”X”]]
输出: [[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”O”,”X”,”X”]]

2.2 思路

先遍历 board 的边界，如果边界上有为 'O' 的格子，将该位置用除了'X'和'O'以外的字符(代码中用'A')进行替换，并按四个方向进行 dfs 搜索，只要搜索到为 'O' 的格子就进行字符替换并继续进行dfs 搜索直至完成整个边界的遍历。然后再对整个 board 进行遍历，只要 board[r][c] == 'A' 说明该格子为边界上的 'O' 或与边界上的 'O' 相连的 'O'，不需要填充为 'X' , 将其复原为 'O' ；遍历到 'O' 的格子说明需要进行填充，将其字符修改为 'X' 。

完整代码如下：

class Solution {
public:
    int m, n;
    void dfs(vector<vector<char>>& board, int row, int col){
        if(row < 0|| col < 0 || row > m-1 || col > n-1 || board[row][col]!='O'){
            return;
        }
        board[row][col] = 'A';
        dfs(board, row+1, col); //沿四个方向搜索
        dfs(board, row-1, col);
        dfs(board, row, col+1);
        dfs(board, row, col-1);
    }
    void solve(vector<vector<char>>& board) {
        m = board.size(), n = board[0].size();
        if(m < 3 || n < 3){
            return;
        }
        for(int r = 0; r < m; r++){ //遍历左右两列
            dfs(board, r, 0);
            dfs(board, r, n -1);
        }
        for(int c = 1; c < n -1; c++){  //遍历上下两行
            dfs(board, 0, c);
            dfs(board, m-1, c);
        }
        for(int r = 0; r < m; r++){     //遍历整个board
            for(int c = 0; c < n; c++){
                if(board[r][c] == 'O'){
                    board[r][c] = 'X';
                }else if(board[r][c] == 'A'){
                    board[r][c] = 'O';
                }
            }
        }
    }
};

3 二进制矩阵中的最短路径

题目链接：1091. 二进制矩阵中的最短路径

3.1 题目描述

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的畅通路径是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

示例1: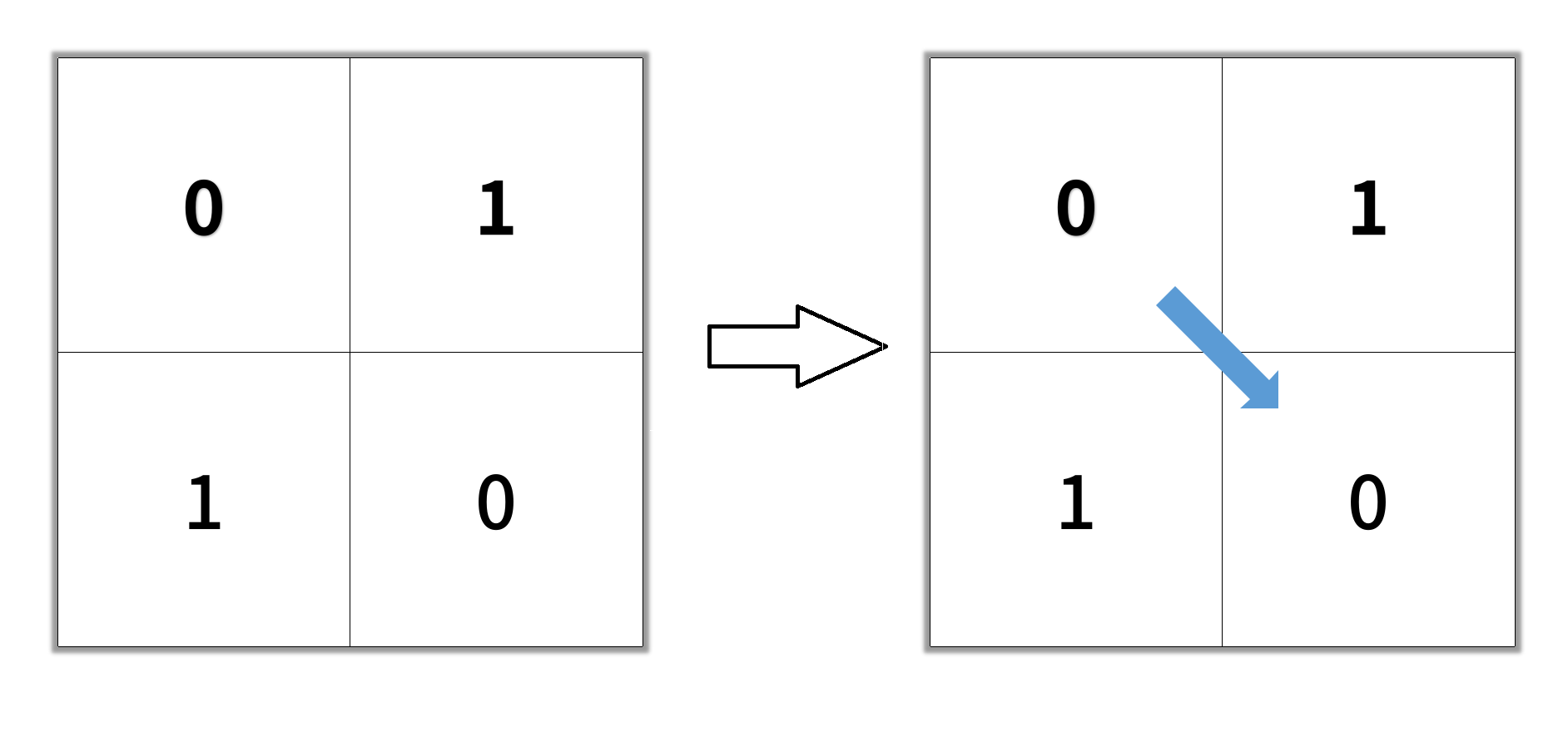

输入: grid = 、[[0,1],[1,0]]
输出: 2

示例2: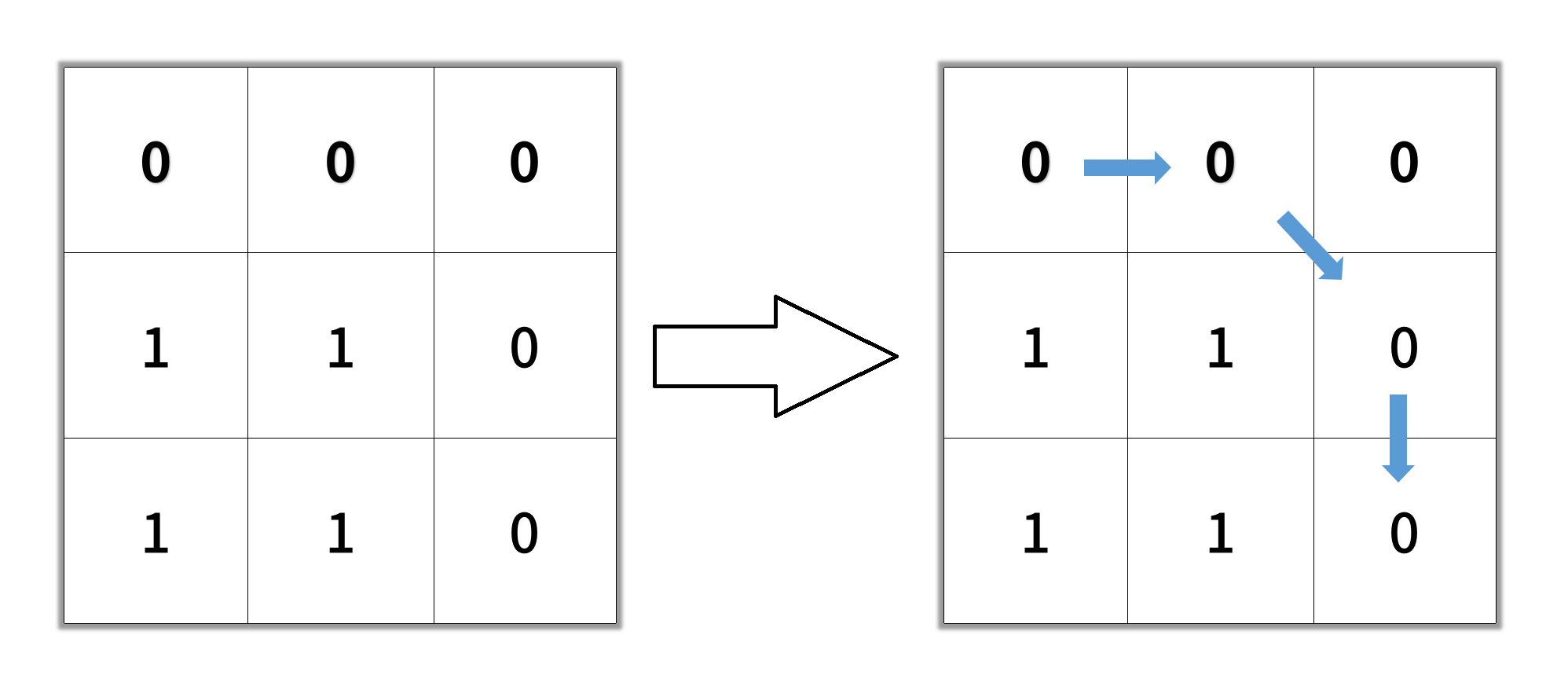

输入: grid = [[0,0,0],[1,1,0],[1,1,0]]
输出: 4

示例3:

输入: grid = [[1,0,0],[1,1,0],[1,1,0]]
输出: -1

3.2 思路

相比深度优先搜索，这一题更适合广度优先搜索，因为题目要求是找到一条 最短的畅通路径 ，而广度优先搜索如果找到目标点(即 右下角 单元格)时的路径即为最短路径，因而采用 广度优先 的方法。
广度优先搜索 的套路是:

1. 建立一个队列
1. 将根节点（起始点）push 到队列
1. 遍历队列直至队列为空，遍历循环中即为我们处理的过程

针对这一题，首先判断起始点或终点是否为 1 ，为 1 说明无法到达终点，直接返回 -1 ;然后进行 bfs ，每遍历一个格子就把该格子置为 1 表明这个格子已经访问过了，避免后边八个方向搜索时往复来回搜索导致heapstack overflow 。

完整代码如下：

class Solution {
public:
    bool isOverstep(int n, int r, int c){
        if(r < 0|| c < 0 || r > n-1 || c > n -1){
            return true;
        }
        return false;
    }

    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        int res = 0;
        int n = grid.size();
        if(grid[0][0] == 1 || grid[n-1][n-1] == 1){
            return -1;
        }
        int dir[8][2] = {{1,1},{1,-1},{-1,1},{-1,-1},{1,0},{0,1},{-1,0},{0,-1}};
        queue<pair<int,int>> q;
        q.push(make_pair(0,0));
        grid[0][0] = 1;
        while(!q.empty()){
            int cnt = q.size();
            while(cnt--){
                auto iter = q.front();
                int row = iter.first, col = iter.second;
                if(row == n-1 && col == n-1){
                    return res+1;
                }
                q.pop();
                for(int i = 0; i < 8; i++){
                    int nextRow = row + dir[i][0], nextCol = col + dir[i][1];
                    if(isOverstep(n, nextRow, nextCol)){
                        continue;
                    }
                    if(grid[nextRow][nextCol] == 0){
                        q.push({nextRow,nextCol});
                        grid[nextRow][nextCol] = 1;
                    }
                }
            }
            ++res;
        }
        return -1;
    }
};

总结

对于矩阵（或者说“图”）的搜索，优先考虑 动态规划，其次再考虑 DFS 和 BFS 。如果要找最短路径，则采用 BFS ，因为 BFS 是从起始点辐射开来，效率会比 DFS 高很多，而如果要找到一条准确的路径，如上边的单词匹配，则采用 DFS 更为方便。
对于搜索问题，谨记：如果某个位置的字符是题目的约束（且只能用一次），那么考虑用一个数组来记录当前遍历过的节点，避免”重蹈覆辙”，亦或者是再原本的 vector 或 matrix 上进行修改！