DDPG

1 DDPG概述

对于连续的动作空间，基于价值的算法(如Q-learning、Sarsa、DQN等)是无能为力的，而基于策略的算法(如Policy Gradient)则可以按照状态给出动作的概率，然后通过某种分布进行采样进而得到对应的动作，可以很好地处理连续动作的问题。

连续控制中较为经典的算法是 深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG) ,它结合了 DQN 的 目标网络 和 经验回放 这两个tips以及 Policy Gradient 处理连续动作空间的优点， 属于 Actor-Critic 的范畴，其中 Policy net 为 Actor ,而 Q-net 则为 Critic。

主要的特点是:

• 与 Policy Gradient 相比， DDPG 采用单个 step 对网络进行更新，即 DDPG 是一个单步更新的 policy 网络。
• 具有与 DQN 类似的 目标网络 和 经验回放， 但 目标网络 的更新是是根据 Policy net 的输出来进行更新。

2 DDPG算法

• Policy Net 的优化

  在 DDPG 中， policy 只根据 q-net 的输出来进行参数 $\theta$ 的优化，而不管实际所获得的 reward 大小；而 q-net 则是根据环境反馈的 reward 来调整参数 $w$ 从而最大化未来的收益。

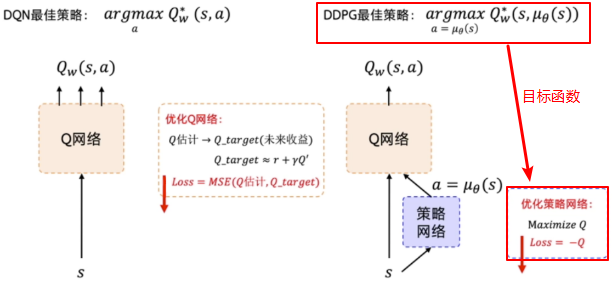
策略梯度中实际上是没有 Loss 的，因为策略梯度输出的是动作的概率。但是我们有目标函数，就是 $Maximisze Q$, 而优化器中一般都是采用梯度下降 Gradient Desent 的方式来对 Loss 进行最小化，因而我们将目标函数转换一下，使之目标转换为找最小值，那么就可以通过已有的优化器来寻求 $Maximisze Q$ 的解了，即定义 Loss = - Q。

• Q Net 的优化

   Q Net 的优化实际上与 DQN 一样，即通过环境反馈的 Reward 以及下个状态中的最大 Q-value 作为未来收益的评估值，目标就是让 Q net 的参数去逼近这个评估值。

• Target Net 建立

  为了解决同 DQN 中Q-target 一直改变导致网络难以收敛的问题，DDPG 中存在策略网络和 Q Net 二者的更新，因此建立两个target net 来稳定Q-target.

• 探索机制

  DDPG 通过 off-policy 的方式来训练一个确定性策略。因为策略是确定的，如果 agent 使用同策略来探索，在一开始的时候，它会很可能不会尝试足够多的 action 来找到有用的学习信号。为了让 DDPG 的策略更好地探索，我们在训练的时候给它们的 action 加了噪音。DDPG 的原作者推荐使用时间相关的 OU noise，但最近的结果表明不相关的、均值为 0 的 Gaussian noise 的效果非常好。为了便于获得更高质量的训练数据，可以在训练过程中把噪声变小。
  在测试的时候，为了查看策略利用它学到的东西的表现，不会在 action 中加噪音。

此段直接摘自EasyRL

3 改进

   DDPG 在超参数和其他类型的调整方面经常很敏感。DDPG 常见的问题是已经学习好的 Q 函数开始显著地高估 Q 值，然后导致策略被破坏了，因为它利用了 Q 函数中的误差。

• Twin Delayed DDPG(TD3)
  • 截断双Q学习(Clipped Double Q-learning): 两个 Q Net ，选择输出小的 Q-value.
  • 延迟的策略更新(“Delayed” Policy Updates)：同步训练动作网络和评价网络，却不使用目标网络，会导致训练过程不稳定；但是仅固定动作网络时，评价网络往往能够收敛到正确的结果。因此 TD3 算法以较低的频率更新动作网络，较高频率更新评价网络，通常每更新两次评价网络就更新一次策略。
  • 目标策略平滑(Target Policy smoothing)：在目标动作中加入噪音. $$a_{TD3}(S^\prime) = clip(\mu_{\theta,targ}(s^\prime)+clip(\epsilon,-c,c), a_{min}, a_{max})$$ 其中$\epsilon \sim N(0,\sigma)$