leetcode-weekly-contest-294

Problem List

• [1] 字母在字符串中的百分比
• [2] 装满石头的背包的最大数量
• [3] 表示一个折线图的最少线段数
• [4] 巫师的总力量和(我不会)

1 字母在字符串中的百分比

1.1 题目描述

• 题目链接：2278. 字母在字符串中的百分比

给你一个字符串 s 和一个字符 letter ，返回在 s 中等于 letter 字符所占的 百分比 ，向下取整到最接近的百分比。

示例1：

输入: s = “foobar”, letter = “o”
输出: 33

示例2：

输入: s = “jjjj”, letter = “k”
输出: 0

1.2 思路

  遍历字符串，当当前字符与l一致时计数器cnt加1, 然后返回cnt*100/s.length()（百分比）即可。

class Solution {
public:
    int percentageLetter(string s, char l) {
        int cnt = 0, n = s.length();
        for(auto c: s){
            if(l == c){
                cnt++;
            }
        }
        return cnt*100/n;
    }
};

2 装满石头的背包的最大数量

2.1 题目描述

• 题目链接：2279. 装满石头的背包的最大数量

现有编号从?0 到 n - 1 的 n 个背包。给你两个下标从 0 开始的整数数组 capacity 和 rocks 。第 i 个背包最大可以装 capacity[i] 块石头，当前已经装了 rocks[i] 块石头。另给你一个整数 additionalRocks ，表示你可以放置的额外石头数量，石头可以往 任意 背包中放置。

请你将额外的石头放入一些背包中，并返回放置后装满石头的背包的 最大 数量。

示例1：

输入: capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
输出: 3

示例2：

输入: capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
输出: 3

2.2 思路

  用一个rest数组来记录每个背包的剩余容量capacity[i]-rock[i],然后对该数组进行排序。遍历该数组，当当前位置不为0则将additionalRocks减去当前背包的剩余容量并将计数器cnt加1，当additionalRocks不够减（变为负）时说明石头已经用完，直接返回即可。

注意：特殊楼层间隔层数要在special[i]-special[i-1]的基础上再减去1，因为不包括两端的边界。

class Solution {
public:
    int maximumBags(vector<int>& c, vector<int>& r, int a) {
        int n = c.size(), cnt = 0;
        vector<int> rest;
        for(int i = 0; i < n; ++i){
            int tmp = c[i] - r[i];
            if(tmp == 0){
                ++cnt;
            }else{
                rest.emplace_back(tmp);
            }
        }
        if(rest.size() == 0) return cnt;
        sort(rest.begin(), rest.end());
        for(int i = 0; i < rest.size(); ++i){
            a -= rest[i];
            if(a < 0){
                break;
            }else{
                ++cnt;
            }
        }
        return cnt;
    }
};

3 表示一个折线图的最少线段数

3.1 题目描述

• 题目链接：2280. 表示一个折线图的最少线段数

给你一个二维整数数组?stockPrices ，其中?stockPrices[i] = [dayi, pricei]?表示股票在?$day_i$?的价格为?$price_i$?。折线图?是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

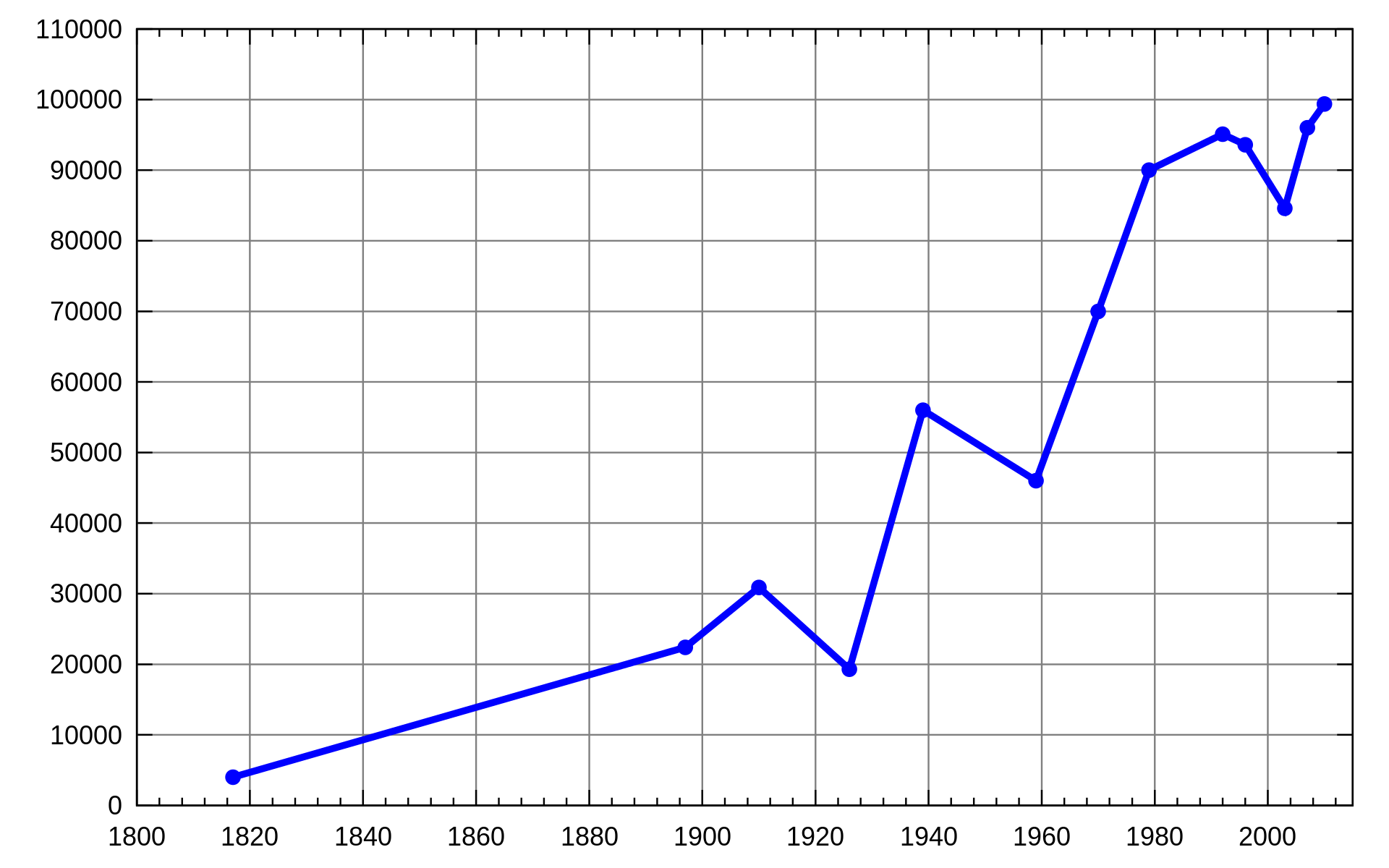
请你返回要表示一个折线图所需要的 最少线段数 。

示例1：

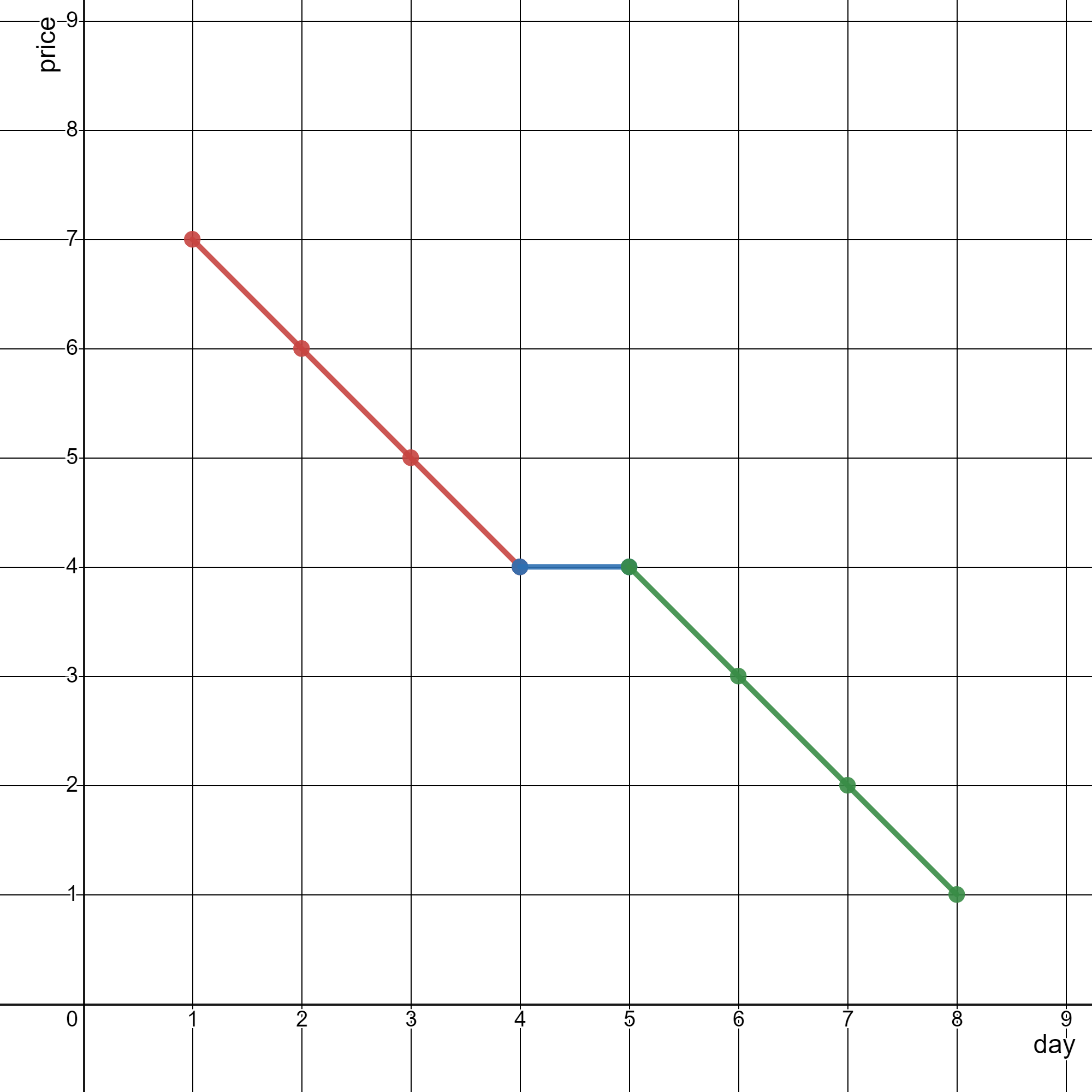
输入: stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出: 3

示例2：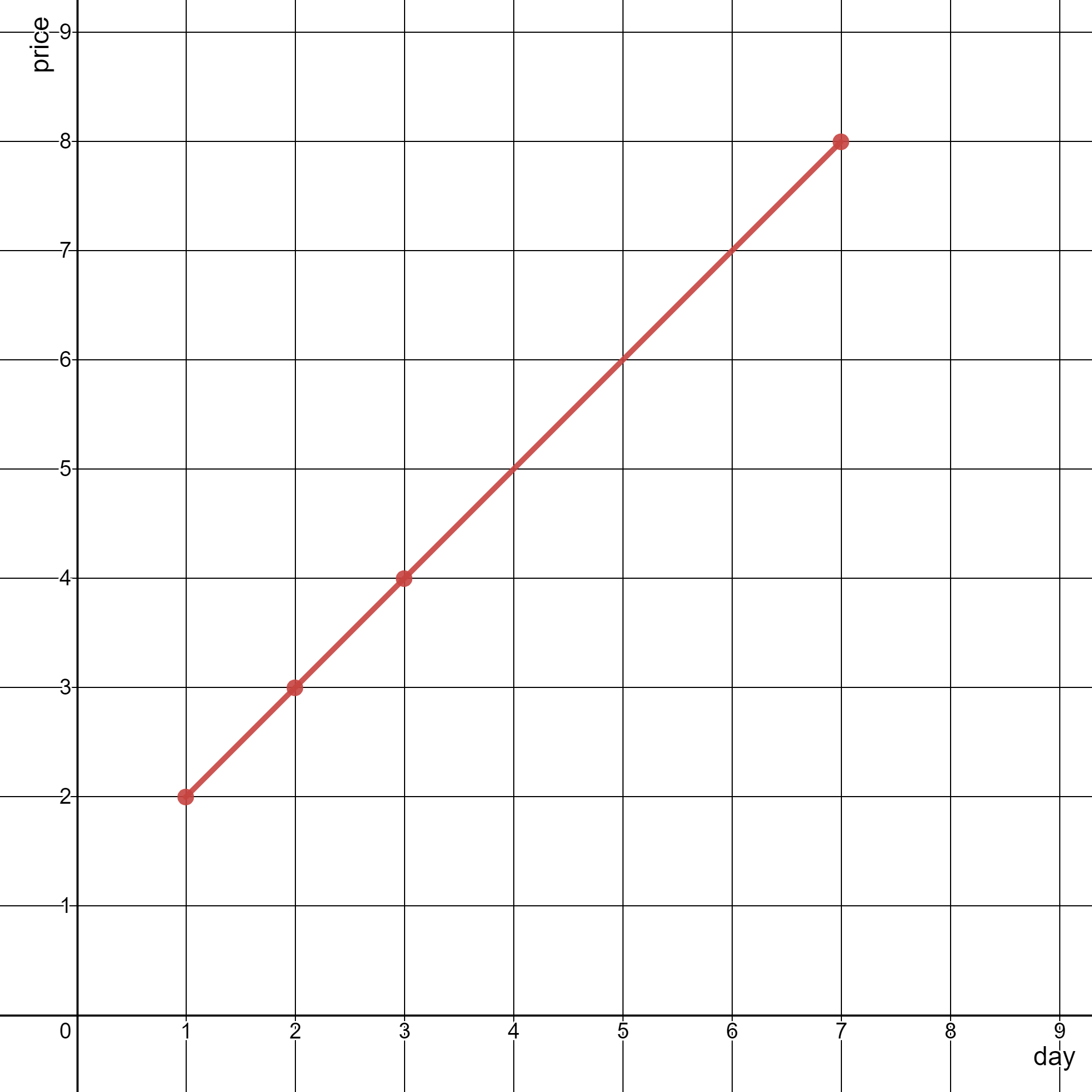

输入: stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出: 1

3.2 思路

  遍历数组，然后求当前节点的左右两端的斜率是否一致即可，这里注意横轴为day，原数组是无序的，因而需要对其进行排序。斜率其实就是$k = \frac{dy}{dx}$, 则用ly和lx表示当前节点左侧的线段在y方向和x方向的变化量，而用ry和rx表示当前节点右侧的线段在y方向和x方向的变化量，那么当满足：

$$ly/lx == ry/rx$$

时当前节点左右两侧的节点共线，由于整型相乘会向下取整，因而对上式进行变换以避免精度导致的误差：

$$ly * rx == ry * lx$$

但需要注意，整型相乘可能会越界，因而需要对其数据类型进行转换，转换为long long型。

class Solution {
public:
    int minimumLines(vector<vector<int>>& s) {
        if(s.size() < 2) return 0;
        sort(s.begin(), s.end());
        /*sort(s.begin(), s.end(), [](const vector<int> a, const vector<int> b){
            return a[0] < b[0];
        });*/
        int cnt = 1;
        for(int i = 1; i+1 < s.size(); ++i){
            int lx = s[i][0]- s[i-1][0], ly = s[i][1]- s[i-1][1]; 
            int rx = s[i+1][0]- s[i][0], ry = s[i+1][1]- s[i][1];
            if(((long long)lx*ry) != ((long long)ly*rx)){
                cnt++;
            }
        }
        return cnt;
    }
};

注意：这里用lambda表达式会超时！！！