Problem List
- [1] 找到一个数字的 K 美丽值
- [2] 分割数组的方案数
- [3] 毯子覆盖的最多白色砖块数
- [4] 最大波动的子字符串(我不会)
1 找到一个数字的 K 美丽值
1.1 题目描述
- 题目链接:2269. 找到一个数字的 K 美丽值
1.1 题目描述
一个整数 num 的 k 美丽值定义为 num 中符合以下条件的 子字符串 数目:
子字符串长度为 k 。
子字符串能整除 num。
给你整数 num 和 k ,请你返回 num 的 k 美丽值。
注意:
允许有 前缀 0 。0 不能整除任何值。
一个 子字符串 是一个字符串里的 连续 一段字符序列。
示例1:
输入: num = 240, k = 2
输出: 2
解释: 以下是 num 里长度为 k 的子字符串:
- “240” 中的 “24” :24 能整除 240 。
- “240” 中的 “40” :40 能整除 240 。
所以,k 美丽值为 2
示例2:
输入: num = 430043, k = 2
输出: 2
解释: 以下是 num 里长度为 k 的子字符串:
- “430043” 中的 “43” :43 能整除 430043 。
- “430043” 中的 “30” :30 不能整除 430043 。
- “430043” 中的 “00” :0 不能整除 430043 。
- “430043” 中的 “04” :4 不能整除 430043 。
- “430043” 中的 “43” :43 能整除 430043 。
所以,k 美丽值为 2 。
1.2 思路
实际上的意思就是输入的数字可以被其长度为k的连续子串所表示的数字整除,因此直接遍历整个字符串,每次取子串然后判断是否可以被整除即可。
class Solution {
public:
int divisorSubstrings(int num, int k) {
string str = to_string(num);
int len = str.length(), cnt = 0;
for(int i = 0; i <= len - k; ++i){
int tmp = 0;
for(int j = 0; j < k; ++j){
tmp *= 10;
tmp += str[i+j]-'0';
}
if(tmp == 0) continue;
else if(num % tmp == 0) cnt++;
}
return cnt;
}
}; 2 分割数组的方案数
2.1 题目描述
- 题目链接:2270. 分割数组的方案数
2.1 题目描述
给你一个下标从 0 开始长度为 n 的整数数组 nums 。
如果以下描述为真,那么 nums 在下标 i 处有一个 合法的分割 :
前 i + 1 个元素的和 大于等于 剩下的 n - i - 1 个元素的和。
下标 i 的右边 至少有一个 元素,也就是说下标 i 满足 0 <= i < n - 1 。
请你返回 nums 中的 合法分割 方案数。
示例1:
输入: nums = [10,4,-8,7]
输出: 2
解释: 总共有 3 种不同的方案可以将 nums 分割成两个非空的部分:
- 在下标 0 处分割 nums 。那么第一部分为 [10] ,和为 10 。第二部分为 [4,-8,7] ,和为 3 。因为 10 >= 3 ,所以 i = 0 是一个合法的分割。
- 在下标 1 处分割 nums 。那么第一部分为 [10,4] ,和为 14 。第二部分为 [-8,7] ,和为 -1 。因为 14 >= -1 ,所以 i = 1 是一个合法的分割。
- 在下标 2 处分割 nums 。那么第一部分为 [10,4,-8] ,和为 6 。第二部分为 [7] ,和为 7 。因为 6 < 7 ,所以 i = 2 不是一个合法的分割。
所以 nums 中总共合法分割方案受为 2 。
示例2:
输入: nums = [2,3,1,0]
输出: 2
解释: 总共有 2 种 nums 的合法分割:
- 在下标 1 处分割 nums 。那么第一部分为 [2,3] ,和为 5 。第二部分为 [1,0] ,和为 1 。因为 5 >= 1 ,所以 i = 1 是一个合法的分割。
- 在下标 2 处分割 nums 。那么第一部分为 [2,3,1] ,和为 6 。第二部分为 [0] ,和为 0 。因为 6 >= 0 ,所以 i = 2 是一个合法的分割。
2.2 思路
遍历整个数组,题目意思就是让以当前遍历到的数字为分界,其左侧子数组的加和大于右侧子数组的加和即为 有效的分割 。因此,可以采用前缀和,先求数组的前缀和(用vec数组来存储前缀和),然后遍历数组,判断vec[i] > vec[n-1]-vec[i]是否成立,若是则说明当前的分割为有效分割,计数器加1,否则不做处理。
需要注意的是,题目中-10^5 <= nums[i] <= 10^5且2 <= nums.length() <= 10^5,因而前缀和(-10,000,000,000~10,000,000,000)可能越界(-2^31 ~ 2^31-1 = -2,147,483,648~2,147,483,647),因而vec的数据类型应该定义为long long。
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int res = 0, n = nums.size();
if(n < 2) return res;
vector<long long> vec(n, 0);
vec[0] = nums[0];
for(int i = 1; i < n; ++i){
vec[i] = vec[i-1] + nums[i];
}
for(int i = 0; i < n-1; ++i){
if(vec[i] < vec[n-1]-vec[i]){
continue;
}
++res;
}
return res;
}
}; 3 毯子覆盖的最多白色砖块数
3.1 题目描述
- 题目链接:2271. 毯子覆盖的最多白色砖块数
3.1 题目描述
给你一个二维整数数组 tiles ,其中 tiles[i] = [li, ri] ,表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。
同时给你一个整数 carpetLen ,表示可以放在 任何位置 的一块毯子。
请你返回使用这块毯子,最多 可以盖住多少块瓷砖。
示例1:
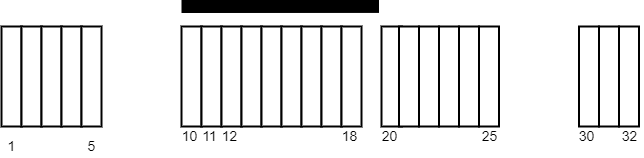
输入: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出: 9
解释: 将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖,所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出,瓷砖无法覆盖超过 9 块瓷砖。
示例2:
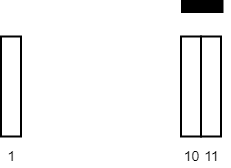
输入: tiles = [[10,11],[1,1]], carpetLen = 2
输出: 2
解释: 将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖,所以我们返回 2 。
3.2 思路
简单的模拟即可,采用前缀和+哈希表的方法进行求解,前缀和用于求从第一个区间到最后一个区间中的瓷砖总数,然后用一个哈希表来存储区间左右端点以及对应的从第一个区间到当前区间的瓷砖数目。用lower_bound来求第一个不在覆盖范围的区间,然后求这个覆盖区间中的瓷砖数,求其最大值即可。
ps: 这道题用线段树更为简单。
class Solution {
map<pair<int, int>, int> m;
public:
int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
sort(tiles.begin(), tiles.end());
int n = tiles.size();
vector<int> vec(n+1, 0);
for(int i = 1; i <= n; ++i){
int tmp = tiles[i-1][1] - tiles[i-1][0] + 1;
if(tmp >= carpetLen) return carpetLen;
vec[i] = vec[i-1] + tmp;
m[make_pair(tiles[i-1][1], tiles[i-1][0])] = vec[i];
}
int res = 0;
for(int i = 1; i <= n; ++i){
auto iter = m.lower_bound(make_pair(tiles[i-1][0]+carpetLen-1, 0));
int tmp = 0;
if(iter == m.end()){
tmp = vec[n] - vec[i-1];
}else{
tmp = iter->second - vec[i-1];
if(iter->first.second > tiles[i-1][0]+carpetLen-1){
tmp -= iter->first.first - iter->first.second + 1;
}else{
tmp -= iter->first.first - (tiles[i-1][0]+carpetLen-1);
}
}
res = max(res, tmp);
}
return res;
}
};
