Problem List
- [1] 判断一个数的数字计数是否等于数位的值
- [2] 最多单词数的发件人
- [3] 道路的最大总重要性
- [4] 以组为单位订音乐会的门票
1 判断一个数的数字计数是否等于数位的值
1.1 题目描述
1.1 题目描述
给你一个下标从 0 开始长度为 n 的字符串 num ,它只包含数字。
如果对于 每个 0 <= i < n 的下标 i ,都满足数位 i 在 num 中出现了 num[i]次,那么请你返回 true ,否则返回 false 。
示例1:
输入: num = “1210”
输出: true
解释: num[0] = ‘1’ 。数字 0 在 num 中出现了一次。
num[1] = ‘2’ 。数字 1 在 num 中出现了两次。
num[2] = ‘1’ 。数字 2 在 num 中出现了一次。
num[3] = ‘0’ 。数字 3 在 num 中出现了零次。
“1210” 满足题目要求条件,所以返回 true 。
示例2:
输入: num = “030”
输出: false
解释: num[0] = ‘0’ 。数字 0 应该出现 0 次,但是在 num 中出现了一次。
num[1] = ‘3’ 。数字 1 应该出现 3 次,但是在 num 中出现了零次。
num[2] = ‘0’ 。数字 2 在 num 中出现了 0 次。
下标 0 和 1 都违反了题目要求,所以返回 false 。
1.2 思路
nums[i]为数字i在数组中出现的次数,可以将数组存放到哈希表中,然后遍历数组,通过哈希查找来求下标数字i在数组中出现的次数,如果为nums[i]则继续遍历直至遍历完成返回true,否则返回false.
class Solution {
unordered_map<int, int> m;
public:
bool digitCount(string num) {
for(char ch: num){
m[ch - '0']++;
}
for(int i = 0; i < num.length(); ++i){
if(num[i]-'0' != m[i]){
return false;
}
}
return true;
}
}; 2 最多单词数的发件人
2.1 题目描述
- 题目链接:2284. 最多单词数的发件人
2.1 题目描述
给你一个聊天记录,共包含 n 条信息。给你两个字符串数组 messages 和 senders ,其中 messages[i] 是 senders[i] 发出的一条 信息 。
一条 信息 是若干用单个空格连接的 单词 ,信息开头和结尾不会有多余空格。发件人的 单词计数 是这个发件人总共发出的 单词数 。注意,一个发件人可能会发出多于一条信息。
请你返回发出单词数 最多 的发件人名字。如果有多个发件人发出最多单词数,请你返回 字典序 最大的名字。
注意:
字典序里,大写字母小于小写字母。"Alice" 和 "alice" 是不同的名字。
示例1:
输入: messages = [“Hello userTwooo”,”Hi userThree”,”Wonderful day Alice”,”Nice day userThree”], senders = [“Alice”,”userTwo”,”userThree”,”Alice”]
输出: “Alice”
解释: Alice 总共发出了 2 + 3 = 5 个单词。
userTwo 发出了 2 个单词。
userThree 发出了 3 个单词。
由于 Alice 发出单词数最多,所以我们返回 “Alice” 。
示例2:
输入: messages = [“How is leetcode for everyone”,”Leetcode is useful for practice”], senders = [“Bob”,”Charlie”]
输出: “Charlie”
解释: Bob 总共发出了 5 个单词。
Charlie 总共发出了 5 个单词。
由于最多单词数打平,返回字典序最大的名字,也就是 Charlie 。
2.2 思路
用哈希表来记录每个用户发送的单词数,由于哈希表本身的具有键有序性。因此,我们只需构造哈希表后遍历哈希表,保存单个用户发送的最多单词数即可,当出现单词数相同且均为最大时,由于哈希表的键有序性,后遍历的用户名的字典序即为最大。
class Solution {
map<string, int> m;
int calNum(string str){
int res = 0;
for(int i = 1; i < str.length(); ++i){
if(str[i] == ' ' && str[i-1] != ' '){
res++;
}
}
return res+1;
}
public:
string largestWordCount(vector<string>& messages, vector<string>& senders) {
int n = messages.size();
for(int i = 0; i < n; ++i){
m[senders[i]] += calNum(messages[i]);
}
int tmp = INT_MIN;
string res = "";
for(auto it: m){
if(it.second >= tmp){
res = it.first;
tmp = it.second;
}
}
return res;
}
}; 3 道路的最大总重要性
3.1 题目描述
- 题目链接:2285. 道路的最大总重要性
3.1 题目描述
给你一个整数 n ,表示一个国家里的城市数目。城市编号为 0 到 n - 1 。
给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条 双向 道路。
你需要给每个城市安排一个从 1 到 n 之间的整数值,且每个值只能被使用 一次 。道路的 重要性 定义为这条道路连接的两座城市数值 之和 。
请你返回在最优安排下,所有道路重要性 之和 最大 为多少。
示例1:
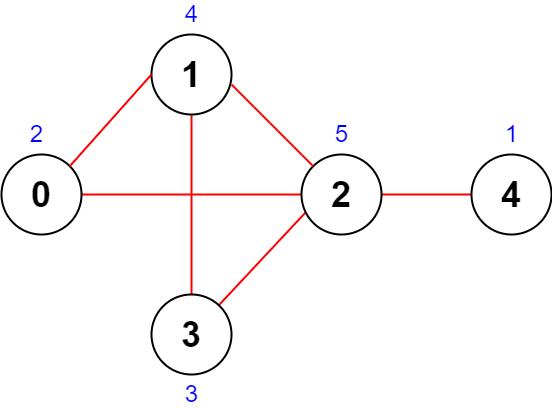
输入: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出: 43
解释: 上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明,重要性之和不可能超过 43 。
示例2:
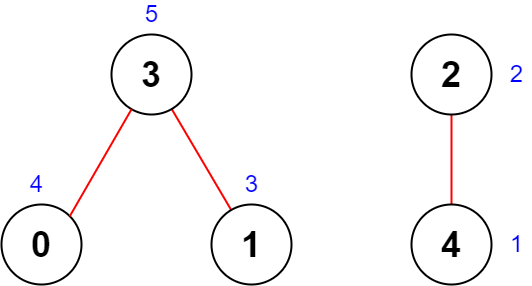
输入: n = 5, roads = [[0,3],[2,4],[1,3]]
输出: 20
解释: 上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明,重要性之和不可能超过 20 。
3.2 思路
道路的重要性为道路两端的城市的数值之和。若要取得最大总重要性,很直觉的想法就是赋予与越多其他城市相连的城市越高的数值即可。思想为贪心+哈希。
class Solution {
public:
long long maximumImportance(int n, vector<vector<int>>& roads) {
vector<int> hash(n, 0);
for(auto it: roads){
hash[it[0]]++;
hash[it[1]]++;
}
sort(hash.begin(), hash.end());
long long res = 0;
for(int i = 1; i <= n; ++i){
res += (long long)i * hash[i-1];
}
return res;
}
}; 4 以组为单位订音乐会的门票
4.1 题目描述
- 题目链接:2286. 以组为单位订音乐会的门票
4.1 题目描述
一个音乐会总共有 n 排座位,编号从 0 到 n - 1 ,每一排有 m 个座椅,编号为 0 到 m - 1 。你需要设计一个买票系统,针对以下情况进行座位安排:
- 同一组的
k位观众坐在 同一排座位,且座位连续 。 k位观众中 每一位 都有座位坐,但他们 不一定 坐在一起。
由于观众非常挑剔,所以:
- 只有当一个组里所有成员座位的排数都 小于等于
maxRow,这个组才能订座位。每一组的maxRow可能 不同 。 - 如果有多排座位可以选择,优先选择 最小 的排数。如果同一排中有多个座位可以坐,优先选择号码 最小 的。
请你实现 BookMyShow 类:
BookMyShow(int n, int m),初始化对象,n是排数,m是每一排的座位数。int[] gather(int k, int maxRow)返回长度为2的数组,表示k个成员中 第一个座位 的排数和座位编号,这k位成员必须坐在 同一排座位,且座位连续 。换言之,返回最小可能的r和c满足第r排中[c, c + k - 1]的座位都是空的,且r <= maxRow。如果 无法 安排座位,返回[]。boolean scatter(int k, int maxRow)如果组里所有k个成员 不一定 要坐在一起的前提下,都能在第0排到第maxRow排之间找到座位,那么请返回true。这种情况下,每个成员都优先找排数 最小 ,然后是座位编号最小的座位。如果不能安排所有k个成员的座位,请返回false。
示例1:
输入: [“BookMyShow”, “gather”, “gather”, “scatter”, “scatter”]
[[2, 5], [4, 0], [2, 0], [5, 1], [5, 1]]
输出: [null, [0, 0], [], true, false]
解释: BookMyShow bms = new BookMyShow(2, 5); // 总共有 2 排,每排 5 个座位。
bms.gather(4, 0); // 返回 [0, 0]
// 这一组安排第 0 排 [0, 3] 的座位。
bms.gather(2, 0); // 返回 []
// 第 0 排只剩下 1 个座位。
// 所以无法安排 2 个连续座位。
bms.scatter(5, 1); // 返回 True
// 这一组安排第 0 排第 4 个座位和第 1 排 [0, 3] 的座位。
bms.scatter(5, 1); // 返回 False
// 总共只剩下 2 个座位。。
4.2 思路
- 模拟,用一个数组
end记录每一行已有的观众数。(超时)
class BookMyShow {
vector<int> end;
int row, col;
int canBookRow;
public:
BookMyShow(int n, int m) {
row = n, col = m;
canBookRow = 0;
for(int i = 0; i < n; ++i){
end.emplace_back(0);
}
}
vector<int> gather(int k, int maxRow) {
int i;
bool flag = false;
for(i = canBookRow; i <= maxRow; ++i){
if(k <= col - end[i]){
flag = true;
break;
}
}
if(flag){
int pos = end[i];
end[i] += k;
if(i == canBookRow && end[i] == col) canBookRow++;
return {i, pos};
}
return {};
}
bool scatter(int k, int maxRow) {
if(((long long)maxRow+1)*col < k) return false;
int tmp = k, c = 0;;
for(c = canBookRow; c <= maxRow; ++c){
if(end[c] < col){
tmp -= (col - end[c]);
if(tmp <= 0) break;
}
}
if(tmp > 0) return false;
for(int i = canBookRow; i <= c; ++i){
if(end[i] < col){
if(k - (col - end[i]) > 0){
k -= col - end[i];
end[i] = col;
canBookRow++;
}else{
end[i] += k;
}
}
if(i==canBookRow && end[i] == col){
canBookRow++;
}
}
return true;
}
};- 线段树+二分
class BookMyShow {
vector<long> sum; // 记录当前节点代表的区间中人数,即被占了的座位数
vector<int> min; // 记录当前节点代表的区间中剩余座位数最多的叶节点,即人数最少的排号
int row, col; // 行数、每一行的座位数
// 函数功能:在第idx行上加上val,即第idx行多了val个人
// 函数外的引用格式:add(1, 1, row, idx, val),前三个参数不变
void add(int root, int left, int right, int idx, int val){
if(left == right){ // 到达叶节点
sum[root] += val; // 叶节点其实就是idx行,直接在其上加上val人
min[root] += val; // 叶节点上min[root]其实就是其本身
return;
}
int mid = left + (right - left) / 2; // 计算中间节点(向下取整)
if(idx <= mid){ // 目标行在当前节点的左侧
add(root*2, left, mid, idx, val);
}else{ // 目标行在右侧
add(root*2+1, mid+1, right, idx, val);
}
sum[root] = sum[root*2]+sum[root*2+1]; // 更新节点上的总人数
min[root] = std::min(min[root*2], min[root*2+1]); // 更新每个节点的最少人数
}
// 函数功能:计算从targetL到targetR区间上的总人数(左闭右闭区间)
// 函数外引用格式:query_sum(1, 1, row, targetL, targetR)
long query_sum(int root, int left, int right, int targetL, int targetR){
// 当前访问的区间已经全部包括在目标区间中,则直接返回该区间的总人数即可
if(targetL<=left && targetR>=right){
return sum[root];
}
int mid = left + (right - left) / 2; // 计算区间中点(向下取整)
long sum = 0L; // 暂存加和
// 三种情况:目标区间全部位于当前区间左侧/右侧以及目标当前区间一部分位于左侧一部分在右侧
// 前两种情况分别访问对应的一侧即可,最后一种则将目标区间分成两部分分别访问两侧
// 因而下面的判断不能用if...else...,而是要两次判断。
if(targetL <= mid){ // 访问左侧区间
sum += query_sum(root*2, left, mid, targetL, targetR);
} //访问右侧区间
if(targetR > mid){
sum += query_sum(root*2+1, mid+1, right, targetL, targetR);
}
return sum;
}
// 函数功能:求能容纳col-val人的最小行的索引,即能人数小于等于val的最小行号
// 函数外引用格式:getIndex(1, 1, row, maxRow+1, col-val)
// 注意线段树的下标从1开始而不是0
int getIndex(int root, int left, int right, int maxRow, int val){
// 当前区间的中最少人的行中人数仍然大于val,则当前区间中没有能够容纳col-val人的行
if(min[root] > val){
return 0;
}
if(left == right) return left; // 叶节点,说明找到对应的行号
int mid = left + (right - left) / 2; // 求当前区间的中点
if(min[root*2] < val){ // 判断左侧是否有可以容纳这些人的行
return getIndex(root*2, left, mid, maxRow, val);
}else if(maxRow > mid){ // 判断是否可以访问右侧
return getIndex(root*2+1, mid+1, right, maxRow, val);
}
return 0; // 线段树编号以1开始,0则作为特殊位用于判断
}
public:
BookMyShow(int n, int m) {
row = n, col = m;
sum = vector<long>(4*n); // 初始化容量为4n
min = vector<int>(4*n);
}
vector<int> gather(int k, int maxRow) {
int idx = getIndex(1, 1, row, maxRow, col-k); // 查询能够容纳k人的行号
if(idx == 0){ // 如果返回行号为0,说明第0到maxRow行中没有可以容纳k人的行
return {};
}
int pos = query_sum(1, 1, row, idx, idx); // 查询该行的人数
add(1, 1, row, idx, k); // 安排k人到该行,进行数据更新
return {idx-1, pos}; // 行号需要-1
}
bool scatter(int k, int maxRow) {
// 计算第0行到第maxRow行的剩余空位,如果空位数小于k,则无法安排,返回false
if((long)col*(maxRow+1) - query_sum(1, 1, row, 1, maxRow+1) < k){
return false;
}
// 求有空位的最低行,有空位即该行最少有一个空位,则该行人数少于col-1
int idx = getIndex(1, 1, row, maxRow+1, col-1);
// 循环,逐行安排人加入
while(1){
int rest = col - query_sum(1, 1, row, idx, idx); // 计算当前遍历到的行的剩余空位
if(k <= rest){ // 待安排的人数少于当前行空位数,直接安排k人在该行即完成
add(1, 1, row, idx, k);
return true;
}
k -= rest; // 把该行占满,并到下一行继续安排人
add(1, 1, row, idx, rest);
++idx;
}
}
};
