leetcode-weekly-contest-290

Cpp 哈希 排序 前缀和 力扣周赛
刷题
发布日期:   2022-06-12

Problem List

1. 多个数组求交集

1.1 题目描述

给你一个二维整数数组 nums ，其中 nums[i] 是由 不同 正整数组成的一个非空数组，按 升序排列 返回一个数组，数组中的每个元素在 nums 所有数组 中都出现过。

示例1：
输入： nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]]
输出： [3, 4]
解释： nums[0] = [3,1,2,4,5]，nums[1] = [1,2,3,4]，nums[2] = [3,4,5,6]，在 nums 中每个数组中都出现的数字是 3 和 4 ，所以返回 [3,4] 。

示例2：
输入： nums = [[1,2,3],[4,5,6]]
输出： []
解释： 不存在同时出现在 nums[0] 和 nums[1] 的整数，所以返回一个空列表 [] 。

1.2 思路

  用一个map来记录每个数字出现的次数，当次数与nums.size()相等时说明该数字在所有的数组中都出现过，因而将该数字插入答案数组中。

class Solution {
    map<int, int> m;
public:
    vector<int> intersection(vector<vector<int>>& nums) {
        vector<int> res;
        int n = nums.size();
        for(int i = 0; i < n; ++i){
            for(int num: nums[i]){
                m[num]++;       // 计数
            }
        }
        for(auto it: m){
            if(it.second == n){
                res.emplace_back(it.first);
            }
        }
        return res;
    }
};

2. 统计圆内格点数目

2.1 题目描述

给你一个二维整数数组 circles ，其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆，返回出现在 至少一个 圆内的 格点数目 。

注意：

  • 格点 是指整数坐标对应的点。
  • 圆周上的点 也被视为出现在圆内的点。

示例1：

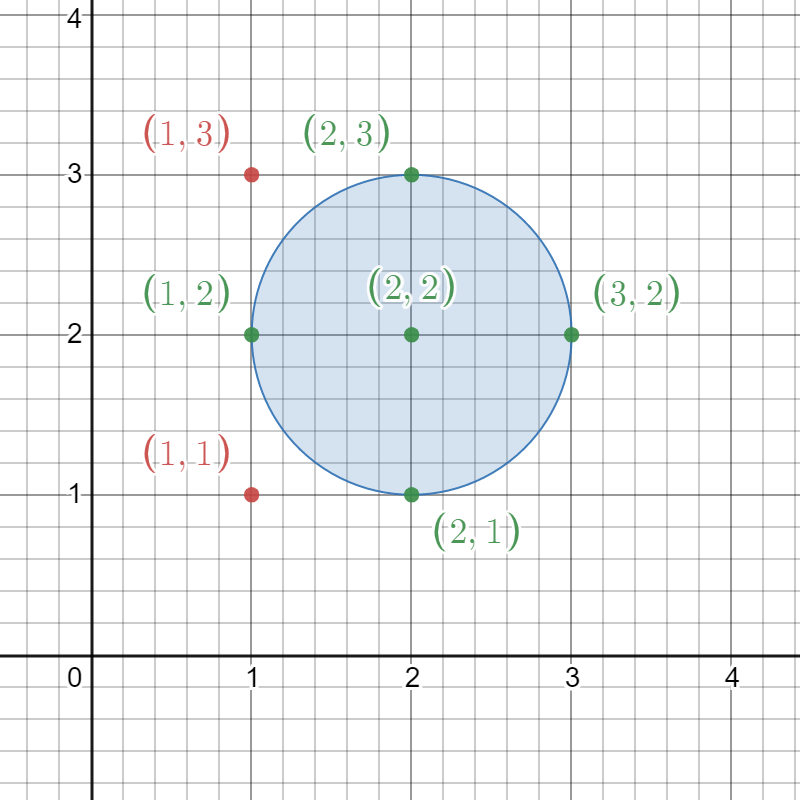
输入： circles = [[2,2,1]]
输出： 5
解释： 给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5 。

示例2：

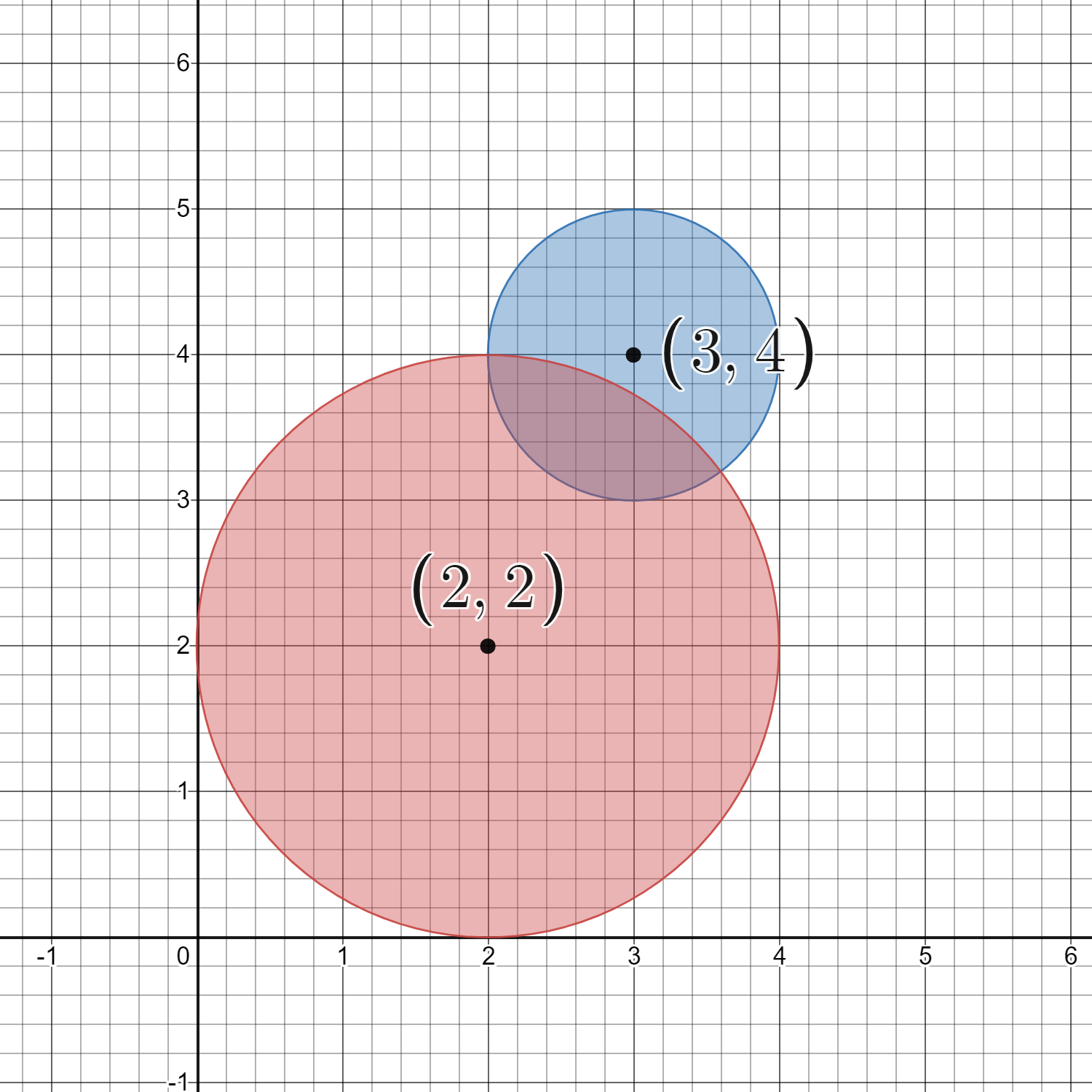
输入： circles = [[2,2,2],[3,4,1]]
输出： 16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。

2.2 思路

  遍历数组，通过圆心坐标、半径大小确定点的横、纵坐标的区间，然后在这个区间中进行坐标遍历，当坐标与圆心的距离小于等于R时将该坐标插入set中，这里使用了set只有单一键的特性，从而滤除重复的坐标，最后返回set.size()即可。

class Solution {
    set<pair<int, int>> s;
public:
    int countLatticePoints(vector<vector<int>>& circles) {
        for(vector<int> circle: circles){
            int l = circle[0], r = circle[0], up = circle[1], low = circle[1];
            l -= circle[2], r += circle[2];
            up += circle[2], low -= circle[2];
            for(int i = l; i <= r; ++i){
                for(int j = low; j <= up; ++j){
                    if((pow(i-circle[0], 2) + pow(j - circle[1], 2)) <= pow(circle[2], 2)){
                        s.insert({i,j});
                    }
                }
            }
        }
        return s.size();
    }
};

3. 统计包含每个点的矩形数目

3.1 题目描述

给你一个二维整数数组 rectangles ，其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ，其中points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。

第 i 个矩形的 左下角 在 (0, 0) 处，右上角 在 (li, hi) 。

请你返回一个整数数组 count ，长度为 points.length，其中 count[j]是 包含 第 j 个点的矩形数目。

如果 0 <= xj <= li 且 0 <= yj <= hi ，那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ，这个点也被视为被矩形包含。

示例1：

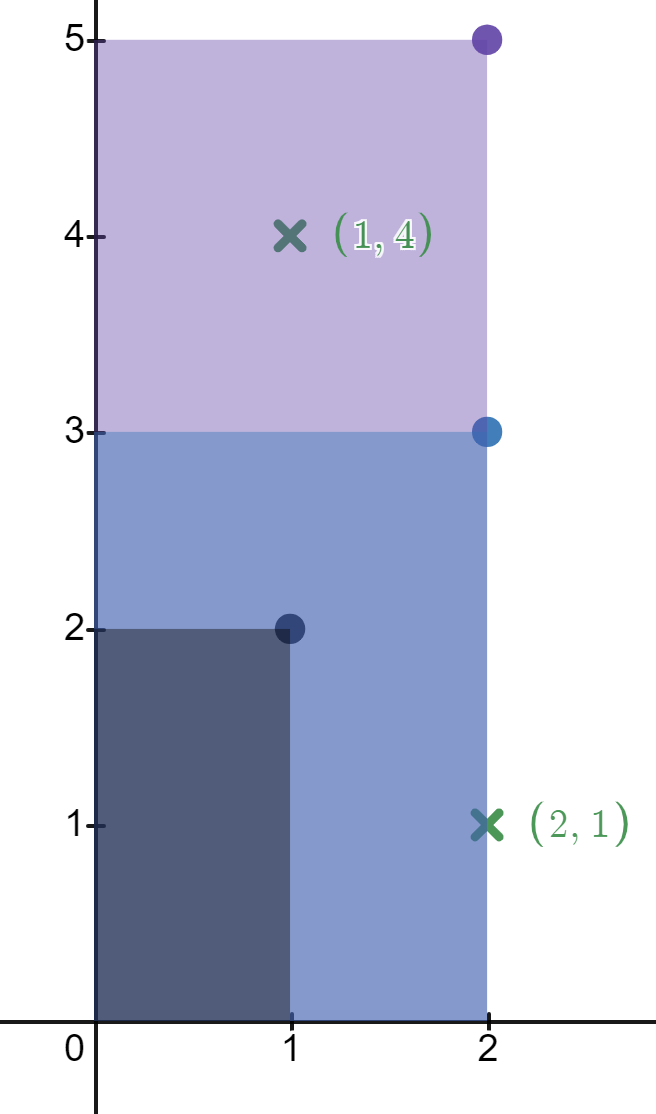
输入： rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
输出： [2, 1]
解释： 第一个矩形不包含任何点。
　第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以，我们返回 [2, 1] 。

示例2：

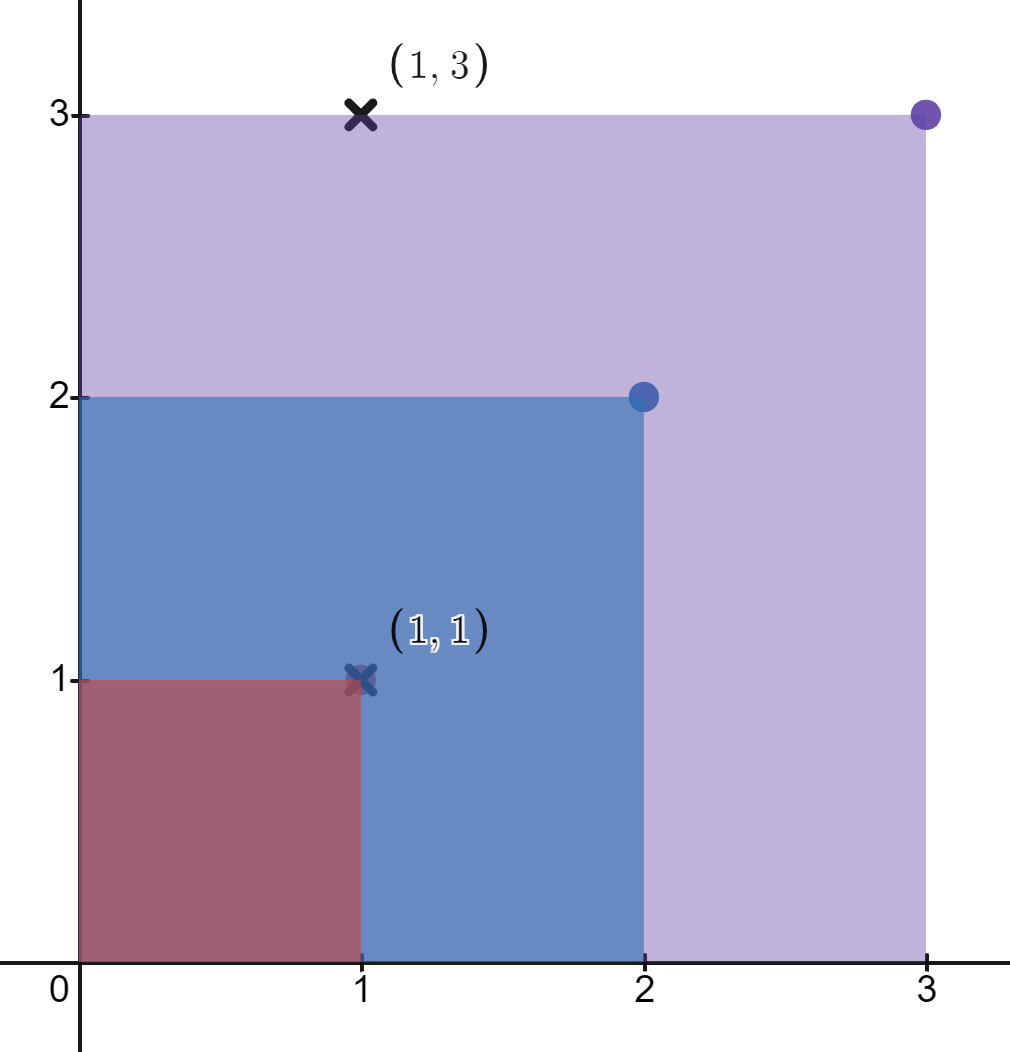
输入： rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
输出： [1, 3]
解释： 第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以，我们返回 [1, 3] 。

提示：

  • 1 <= rectangles.length, points.length <= 5 * 1e4
  • rectangles[i].length == points[j].length == 2
  • 1 <= li, xj <= 1e9
  • 1 <= hi, yj <= 100
  • 所有 rectangles 互不相同 。
  • 所有 points 互不相同 。

3.2 思路

  • 按纵坐标归类

  直接暴力，复杂度最差为2.5e9必定超时。而坐标的纵坐标在1-100的范围内，因此可以从这个地方入手。首先创建一个数组用来存放横坐标，其下标索引为纵坐标，然后遍历整个rectangles数组，将遍历到的坐标的横坐标存到对应的数组中，然后对每一个存放横坐标数组进行升序排序。然后遍历points数组，通过lower_bound找到每个横坐标数组中第一个大于points[i][0]的索引i，则该数组中包含这个点的矩形数量就可以由arr.size() - i得到(arr表示当前遍历的横坐标数组)，对全部横坐标数组进行求和即得到含有该点的矩形数。

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        /*sort(rectangles.begin(), rectangles.end(), [](auto a, auto b){
            if(a[1] == b[1])  return a[0] < b[0];
            return a[1] < b[1];
        });*/
        vector<vector<int>> rec(101);
        for(vector<int> vec: rectangles){
            rec[vec[1]].emplace_back(vec[0]);
        }
        for(int i = 0; i < 101; i++){
            sort(rec[i].begin(), rec[i].end());
        }
        vector<int> res;
        for(vector<int> it: points){
            int sum = 0;
            for(int i = it[1]; i <=100; i++){
                sum += rec[i].end() - lower_bound(rec[i].begin(), rec[i].end(), it[0]);
            }
            res.emplace_back(sum);
        }
        return res;
    }
};

上述过程中需要对每个横坐标数组进行排序，也可以直接对rectangles数组进行排序，但需要使用lambda表达式，实测lambda表达式进行排序的速度比原来的sort慢了不少。

  • 按纵坐标排序

  对rectangles按纵坐标进行降序排序，同样对points进行操作，但注意的是，排完序要记住原来的索引，这个可以用multiset来实现。然后利用前缀和的思想，类似于下道题的处理方式，从points纵坐标最大的点开始遍历，如果当前矩形的纵坐标大于等于这个点的纵坐标则将该点插入到暂存数组中；遍历完成后这个数组中的坐标的纵坐标必定大于等于当前遍历的点的纵坐标，而横坐标则有可能小于这个点的横坐标，因此对这个暂存数组进行升序排序，然后用lower_bound找到点的横坐标在这个数组的位置，从而就可以得到横坐标大于这个点的矩形数目了。

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        sort(rectangles.begin(), rectangles.end(), [](auto p1, auto p2){
            return p1[1] > p2[1];   // 按纵坐标升序排序
        });
        int n = points.size();
        multimap<int, int> m;       // 用multimap来保存纵坐标与原来索引的映射
        vector<int> ids(n);         // 用于保存排序后原来的索引顺序
        // 实现键值映射
        for(int i = 0; i < n; ++i){
            m.insert(make_pair(points[i][1], i));
        }
        // 实现坐标排序后将原索引顺序存放到ids中
        int idx = n-1;              // multimap中是从小到大，因而从大到小需要从后向前存
        for(auto it: m){
            ids[idx--] = it.second;
        }
        vector<int> tmp, ans(n);    // tmp数组用于暂存纵坐标满足大于等于当前点的纵坐标的矩形
        idx = 0;                    // 当前tmp中的矩形数
        for(int id: ids){
            int start = idx;        
            // 当纵坐标满足大于等于当前点，则将其插入暂存数组中
            while(idx < rectangles.size() && rectangles[idx][1] >= points[id][1]){
                tmp.emplace_back(rectangles[idx++][0]);
            }
            // 只有当有新插入的矩形时才进行排序
            if(idx > start){
                sort(tmp.begin(), tmp.end());
            }
            // 用lower_bound找到满足大于等于当前点横坐标的索引，即可求得矩形数
            ans[id] = tmp.end() - lower_bound(tmp.begin(), tmp.end(), points[id][0]);
        }
        return ans;
    }
};

上述代码中使用了multimap来保存坐标与索引的映射，其实也可以通过下面代码来实现：

int n = points.size();
vector<int> ids(n);
iota(ids.begin(), ids.end(), 0);  // 创建一个0为起点，间隔为1的等差数组，即为索引
sort(ids.begin(), ids.end(), [&](const int i, const int j){
    return points[i][0] > points[j][0];   // 采用引用+lambda排序的方法
});

  • 按横坐标排序

  这种做法有点像上边两种做法的结合，通过对横坐标进行升序排序，然后用一个数组来计算横坐标大于等于当前点的横坐标的矩形数，而数组的下标则定义为矩形的纵坐标，从而进行分类，最后求数组中下标从cnt.begin() + points[i][1]到cnt.end()的元素加和即可。

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        sort(rectangles.begin(), rectangles.end(), [](auto p1, auto p2){
            return p1[0] > p2[0];
        });
        int n = points.size();
        vector<int> ids(n);
        iota(ids.begin(), ids.end(), 0);
        sort(ids.begin(), ids.end(), [&](const int i, const int j){
            return points[i][0] > points[j][0];
        });
        vector<int> cnt(101), ans(n);
        int idx = 0;
        for(int id: ids){
            int start = idx;
            while(idx < rectangles.size() && rectangles[idx][0] >= points[id][0]){
                ++cnt[rectangles[idx++][1]];
            }
            ans[id] = accumulate(cnt.begin() + points[id][1], cnt.end(), 0);
            
        }
        return ans;
    }
};

4. 花期内花的数目

4.1 题目描述

给你一个下标从 0 开始的二维整数数组 flowers ，其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti到 endi （都 包含）。同时给你一个下标从 0 开始大小为 n 的整数数组 persons ，persons[i] 是第 i 个人来看花的时间。

请你返回一个大小为 n 的整数数组 answer ，其中 answer[i]是第 i 个人到达时在花期内花的 数目 。

示例1：

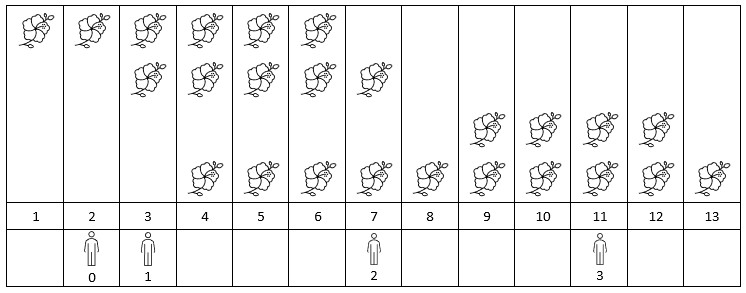
输入： flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
输出： [1, 2, 2, 2]
解释： 上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

示例2：

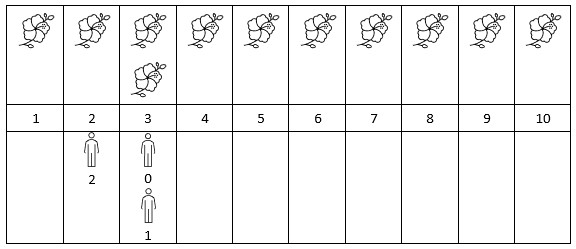
输入： flowers = [[1,10],[3,3]], persons = [3,3,2]
输出： [2, 2, 1]
解释： 上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

4.2 思路

  将日期视为时间轴，要求某个人到达时在花期内花的数目，其实就是求某个人到达时绽放的花的种数，而flowers[i] = [starti, endi]表示的花期在时间上的表示可以转换为在starti时+1，在endi+1时-1，即表示starti时这种花开了，在endi+1天时凋谢，那么转换后如果要求某个人到达时花的种数则可以直接求前缀和即可。

  将问题转换为前缀和的问题，这里可以将人到达的时间做升序排序，从而实现在求答案时顺便求前缀和。

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        map<int, int> diff;
        for(vector<int> it: flowers){
            diff[it[0]]++;      // 开花
            diff[it[1]+1]--;    // 凋谢
        }
        // 不能直接对persons进行排序，因为我们需要原来的顺序对应的索引
        // 用一个pair实现值与下标的映射
        vector<pair<int, int>> id;  
        for(int i = 0; i < persons.size(); ++i){
            id.push_back({persons[i], i});
        }
        // 按升序排序
        sort(id.begin(), id.end());
        vector<int> res(persons.size());
        int sum = 0;    // 前缀和
        auto it = diff.begin();
        for(pair<int,int> i: id){
            while(it != diff.end() && it->first <= i.first){
                sum += it->second;
                ++it;
            }
            res[i.second] = sum;
        }
        return res;
    }
};

复盘

  这次周赛难度比较大，并且使用了之前没用过的两个语句：

  1. 求数组加和：

  • accumulate(iterator* start, iterator* end, bias): 参数依次为累加的元素起始地址、结束地址以及累加的初值，最后一个参数理解为累加前先加上bias后再进行累加， 通常bias为0。

  • accumulate也能实现连乘积，此时有四个参数，前三个参数一致，最后一个则是一个函数，即multiplies<int>(). 此时bias一般设为1.

  • 此外，也可以用于字符串合并.

    std::vector<int> numbers {1, 2, 3, 10, 11, 12};
// 参数顺序：begin, end, bias, operation（func）
auto s = std::accumulate(std::begin(numbers), std::end(numbers),string {"The numbers are"},[](strings str, int n){ return str + " : " + std::to_string(n);});
std::cout << s << std::endl;//Output: The numbers are: 1: 2: 3: 10: 11: 12

  1. 排序后按排序后的结果输出原数组下标顺序

    int n = points.size();
vector<int> ids(n);
iota(ids.begin(), ids.end(), 0);
sort(ids.begin(), ids.end(), [&](const int i, const int j){
    return points[i][0] > points[j][0];
});
文章作者: Vyron Su
文章链接: http://example.com/2022/06/12/leetcode-weekly-contest-290/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Vyron Su !
Cpp 哈希 排序 前缀和 力扣周赛