Problem List
- [1] 兼具大小写的最好英文字母
- [2] 个位数字为 K 的整数之和
- [3] 小于等于 K 的最长二进制子序列
- [4] 卖木头块
1. 兼具大小写的最好英文字母
1.1 题目描述
给你一个由英文字母组成的字符串 s ,请你找出并返回 s 中的 最好 英文字母。返回的字母必须为大写形式。如果不存在满足条件的字母,则返回一个空字符串。
最好 英文字母的大写和小写形式必须 都 在 s 中出现。
英文字母 b 比另一个英文字母 a 更好 的前提是:英文字母表中,b 在 a 之 后 出现。
示例1:
输入: s = “lEeTcOdE”
输出: “E”
解释: 字母 ‘E’ 是唯一一个大写和小写形式都出现的字母。示例2:
输入: s = “arRAzFif”
输出: “R”
解释:
字母 ‘R’ 是大写和小写形式都出现的最好英文字母。
注意 ‘A’ 和 ‘F’ 的大写和小写形式也都出现了,但是 ‘R’ 比 ‘F’ 和 ‘A’ 更好。示例3:
输入: s = “AbCdEfGhIjK”
输出: “”
解释:
不存在大写和小写形式都出现的字母。
1.2 思路
翻译过来就是在字符串中找到大小写均出现过的字母,如果存在多个大小写均出现过的字母,则返回字母表中靠后的那个。那么可以直接对字母表进行遍历,通过find()来查找该字母的大小写在字符串中的出现位置,如果返回的值小于字符串的长度则说明该字母在字符串中出现过,因而更新答案即可。
class Solution {
public:
string greatestLetter(string s) {
string ans;
for(char ch = 'a'; ch <= 'z'; ++ch){
if(s.find(ch)<s.length() && s.find(ch-32)<s.length()){
ans = "";
ans += ch-32;
}
}
return ans;
}
}; 2. 个位数字为 K 的整数之和
2.1 题目描述
给你两个整数 num 和 k ,考虑具有以下属性的正整数多重集:
每个整数个位数字都是 k 。
所有整数之和是 num 。
返回该多重集的最小大小,如果不存在这样的多重集,返回 -1 。
注意:
多重集与集合类似,但多重集可以包含多个同一整数,空多重集的和为 0 。
个位数字 是数字最右边的数位。
示例1:
输入: num = 58, k = 9
输出: 2
解释: 多重集 [9,49] 满足题目条件,和为 58 且每个整数的个位数字是 9 。
另一个满足条件的多重集是 [19,39] 。
可以证明 2 是满足题目条件的多重集的最小长度。
示例2:
输入: num = 37, k = 2
输出: -1
解释: 个位数字为 2 的整数无法相加得到 37 。
示例3:
输入: num = 0, k = 7
输出: 0
解释: 空多重集的和为 0 。
2.2 思路
这一题的数是可以重复取的,所以可以从低位入手,如果低位满足加和等于目标数的低位,则高位就必定可以满足加和后等于目标数。
那么题目就简化为求多少个k的加和后个位数等于num的个位数,即nk%10 == num % 10。
进一步将题目转换为:如果能找到一个n <= 10,使得nk%10 == num % 10成立,则n即为所求答案。
这里考虑一下为什么是n <= 10而不是n <= 9即n < 10. (k==1时而num==10).
接下来就是特殊情况的判定:
- 当num为0时,则不需要加和即为答案,即返回0;
- 当num不为0时
- 找不到一个n <= 10使得 n*k%10 == num % 10成立,说明无法通过个位为k的数加和后等于num,如k == 2,而num为奇数的情况,那么就是返回-1。
- 找到了一个n <= 10使得 nk%10 == num % 10成立,但这个n却使得nk > num成立,这种情况实际上就是单单用n个k加和后已经比目标数大了,如k = 3而num = 17, 那么找到的n为9,但3*9 > 17,所以实际上也是无法构成num的,返回-1.
- 除了上边的情况,n就是答案了,可以推出不存在其他的情况,返回n。
class Solution {
public:
int minimumNumbers(int num, int k) {
if(num == 0){
return 0;
}
int i = 1;
for(; i <= 10; i++){
if(num%10 == i*k%10){
break;
}
}
if(i > 10 || i*k > num) return -1;
return i;
}
}; 3. 小于等于 K 的最长二进制子序列
3.1 题目描述
给你一个二进制字符串 s 和一个正整数 k 。
请你返回 s 的 最长 子序列,且该子序列对应的 二进制 数字小于等于 k 。
注意:
子序列可以有 前导 0 。
空字符串视为 0 。
子序列 是指从一个字符串中删除零个或者多个字符后,不改变顺序得到的剩余字符序列。
示例1:
输入: s = “1001010”, k = 5
输出: 5
解释: s 中小于等于 5 的最长子序列是 “00010” ,对应的十进制数字是 2 。
注意 “00100” 和 “00101” 也是可行的最长子序列,十进制分别对应 4 和 5 。
最长子序列的长度为 5 ,所以返回 5 。
示例2:
输入: s = “00101001”, k = 1
输出: 6
解释: “000001” 是 s 中小于等于 1 的最长子序列,对应的十进制数字是 1 。
最长子序列的长度为 6 ,所以返回 6 。
3.2 思路
贪心,从低位进行遍历,如果为当前位为1则将k将去这个位(转成十进制), k不够当前位减,说明这个位以及后续的位如果为1则需要把这个位删去,最后返回s.length()减去删去的位数即可。
class Solution {
public:
int longestSubsequence(string s, int k) {
int bit = 1, i = s.length()-1;
for(; k >= bit && i >= 0; --i){
if(s[i] == '1') k -= bit;
bit <<= 1;
}
int cnt = 0;
for(; i >= 0; --i){
if(s[i] == '1'){
cnt++;
}
}
return s.length() - cnt;
}
}; 4. 卖木头块
4.1 题目描述
给你两个整数 m 和 n ,分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ,其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。
每一次操作中,你必须按下述方式之一执行切割操作,以得到两块更小的矩形木块:
沿垂直方向按高度 完全 切割木块,或
沿水平方向按宽度 完全 切割木块
在将一块木块切成若干小木块后,你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能 旋转切好后木块的高和宽。
请你返回切割一块大小为 m x n 的木块后,能得到的 最多 钱数。
注意你可以切割木块任意次。
示例1:
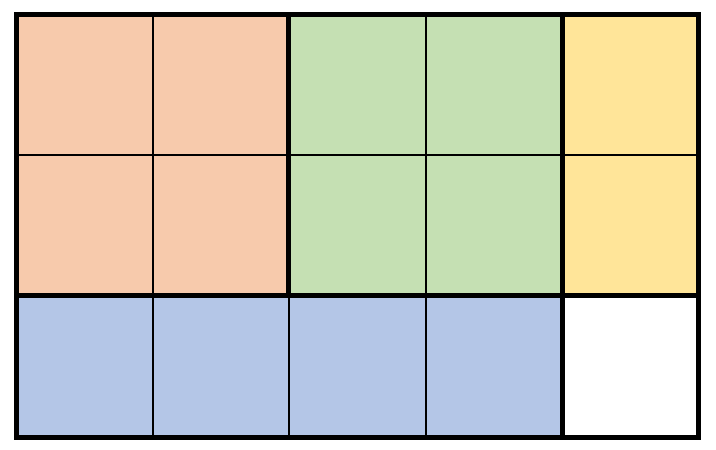
输入: m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出: 19
解释: 上图展示了一个可行的方案。包括:
- 2 块 2 x 2 的小木块,售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块,售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。示例2:
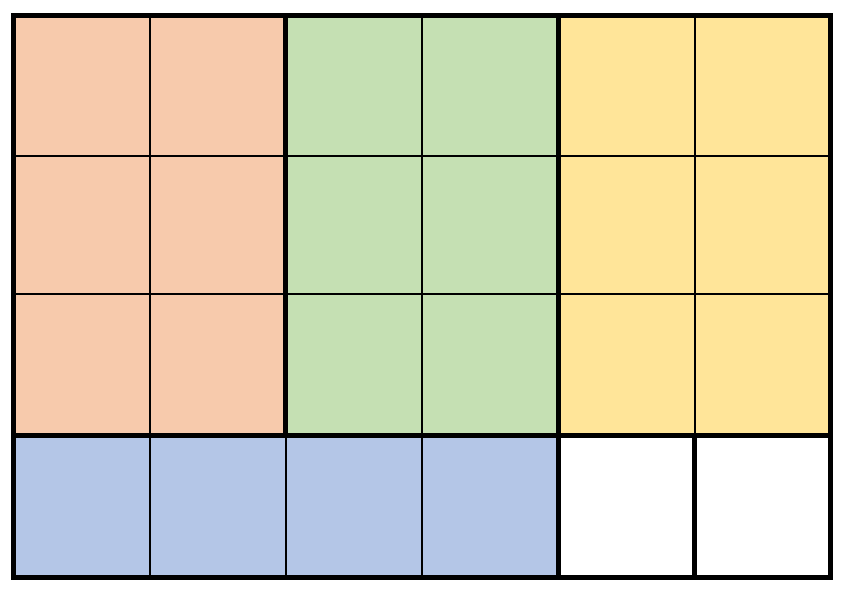
输入: m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出: 32
解释: 上图展示了一个可行的方案。包括:
- 3 块 3 x 2 的小木块,售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。
4.2 思路
背包问题,分成两个方向进行切割。
class Solution {
public:
long long sellingWood(int m, int n, vector<vector<int>>& prices) {
long long dp[201][201] = {0};
for(auto price: prices){
dp[price[0]][price[1]] = price[2];
}
for(int h = 1; h <= m; ++h){
for(int w = 1; w <= n; ++w){
for(int ww = 1; ww <= w; ++ww){
dp[h][w] = max(dp[h][w], dp[h][ww] + dp[h][w - ww]);
}
for(int hh = 1; hh <= h; ++hh){
dp[h][w] = max(dp[h][w], dp[hh][w] + dp[h - hh][w]);
}
}
}
return dp[m][n];
}
}; 复盘
脑子已经不够用了,临场反应拉的一批,情况考虑不全面!!!

