Problem List
- [1] 统计星号
- [2] 统计无向图中无法互相到达点对数
- [3] 操作后的最大异或和
- [4] 不同骰子序列的数目
1. 统计星号
1.1 题目描述
给你一个字符串 s ,每 两个 连续竖线 '|' 为 一对 。换言之,第一个和第二个 '|' 为一对,第三个和第四个 '|' 为一对,以此类推。
请你返回 不在 竖线对之间,s 中 '*' 的数目。
注意,每个竖线 '|' 都会 恰好 属于一个对.
示例1:
输入: ps = “l|eet|co|*de|” 输出: 2 解释:* 不在竖线对之间的字符加粗加斜体后,得到字符串:”l|\e*et|c**o|*de|” 。
第一和第二条竖线 ‘|’ 之间的字符不计入答案。
同时,第三条和第四条竖线 ‘|’ 之间的字符也不计入答案。
不在竖线对之间总共有 2 个星号,所以我们返回 2 。示例2:
输入: s = “iamprogrammer”
输出: 0
解释: 在这个例子中,s 中没有星号。所以返回 0 。示例3:
输入: s = “yo|uar|e**|b|e***au|tifu|l”
输出: 5
解释: 需要考虑的字符加粗加斜体后:”yo|uar|e**|b|e***au|tifu|l” 。不在竖线对之间总共有 5 个星号。所以我们返回 5 。
1.2 思路
用一个变量来存储当前遍历的位置是否在竖线对中,可以通过计算竖线的数量,当为奇数则在竖线对中,为偶数则不在;或者用一个bool变量,并初始化为false,当检测到竖线且此时改变量为false则将变量改为true说明此时在竖线对中,而变量为true时则置为false表示不在竖线对中。然后当不在竖线对中就计数即可。
class Solution {
public:
int countAsterisks(string s) {
int len = s.length(), ans = 0;
bool flag = false;
for(int i = 0; i < len; ++i){
if(!flag && s[i] == '*'){
ans++;
}else if(s[i] == '|'){
if(!flag){
flag = true;
}else{
flag = false;
}
}
}
return ans;
}
};简化以上程序:
class Solution {
public:
int countAsterisks(string s) {
int len = s.length(), ans = 0;
bool flag = false;
for(int i = 0; i < len; ++i){
if(s[i] == '*' && !flag) ans++;
if(s[i] == '|') flag ^= 1;
}
return ans;
}
}; 2. 统计无向图中无法互相到达点对数
2.1 题目描述
给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例1: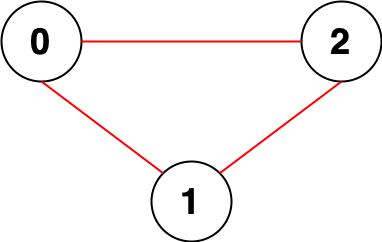
输入: n = 3, edges = [[0,1],[0,2],[1,2]]
输出: 0
解释: 所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
示例2: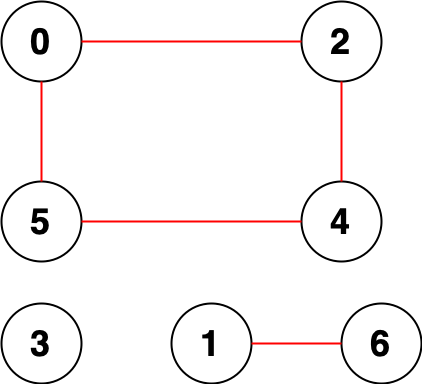
输入: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出: [2, 0, 2]
解释: 总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
2.2 思路
bfs或者dfs均可,大佬都是用并查集但是并查集我不会。
- bfs
class Solution {
vector<vector<int>> vec;
vector<bool> vis;
int bfs(int index){
int cnt = 0;
queue<int> q;
q.push(index);
vis[index] = true;
while(!q.empty()){
int parent = q.front();
cnt++;
q.pop();
for(int it: vec[parent]){
if(!vis[it]){
q.push(it);
vis[it] = true;
}
}
}
return cnt;
}
public:
long long countPairs(int n, vector<vector<int>>& edges) {
vec = vector<vector<int>>(n);
vis = vector<bool>(n, false);
for(int i = 0; i < edges.size(); ++i){
vec[edges[i][0]].emplace_back(edges[i][1]);
vec[edges[i][1]].emplace_back(edges[i][0]);
}
long long ans = 0;
for(int i = 0; i < n; ++i){
int cnt = 0;
if(!vis[i]){
cnt = bfs(i);
}
ans += 1ll*cnt*(n-cnt);
}
return ans/2;
}
};- dfs
class Solution {
vector<vector<int>> vec;
vector<bool> vis;
int dfs(int index, int cnt){
if(vis[index]) return cnt;
vis[index] = true;
cnt++;
for(int i: vec[index]){
cnt += dfs(i, 0);
}
return cnt;
}
public:
long long countPairs(int n, vector<vector<int>>& edges) {
vec = vector<vector<int>>(n);
vis = vector<bool>(n, false);
for(int i = 0; i < edges.size(); ++i){
vec[edges[i][0]].emplace_back(edges[i][1]);
vec[edges[i][1]].emplace_back(edges[i][0]);
}
long long ans = 0;
for(int i = 0; i < n; ++i){
int cnt = 0;
if(!vis[i]){
cnt = dfs(i, 0);
}
ans += 1ll*cnt*(n-cnt);
}
return ans/2;
}
}; 3. 操作后的最大异或和
3.1 题目描述
给你一个下标从 0 开始的整数数组 nums 。一次操作中,选择 任意 非负整数 x 和一个下标 i ,更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。
注意,AND 是逐位与运算,XOR 是逐位异或运算。
请你执行 任意次 更新操作,并返回 nums 中所有元素 最大 逐位异或和。
示例1:
输入: nums = [3,2,4,6]
输出: 7
解释: 选择 x = 4 和 i = 3 进行操作,num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。
现在,nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。
可知 7 是能得到的最大逐位异或和。
注意,其他操作可能也能得到逐位异或和 7 。
示例2:
输入: nums = [1,2,3,9,2]
输出: 11
解释: 执行 0 次操作。
所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。
可知 11 是能得到的最大逐位异或和。
3.2 思路
考虑对一个数进行nums[i] 为 nums[i] AND (nums[i] XOR x)操作:
- 当当前位为0,进行操作之后只会维持为0.
- 当当前位为1,进行操作之后可以变为0,或者维持为1.
那么要得到操作后最大异或结果,那么就是保留每一个位置上的1,其他数字对应位变为0即可,这样就是全部数字按位或就是答案。
class Solution {
public:
int maximumXOR(vector<int>& nums) {
int ans = 0;
for(int i = 0; i < nums.size(); ++i){
ans |= nums[i];
}
return ans;
}
}; 4. 不同骰子序列的数目
4.1 题目描述
给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下,求出 不同 骰子序列的数目:
序列中任意 相邻 数字的 最大公约数 为 1 。
序列中 相等 的值之间,至少有 2 个其他值的数字。正式地,如果第 i 次掷骰子的值 等于 第 j 次的值,那么 abs(i - j) > 2 。
请你返回不同序列的 总数目 。由于答案可能很大,请你将答案对 109 + 7 取余 后返回。
如果两个序列中至少有一个元素不同,那么它们被视为不同的序列。
示例1:
输入: n = 4
输出: 184
解释: 一些可行的序列为 (1, 2, 3, 4) ,(6, 1, 2, 3) ,(1, 2, 3, 1) 等等。
一些不可行的序列为 (1, 2, 1, 3) ,(1, 2, 3, 6) 。
(1, 2, 1, 3) 是不可行的,因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 (下标从 1 开始表示)。
(1, 2, 3, 6) i是不可行的,因为 3 和 6 的最大公约数是 3 。
总共有 184 个不同的可行序列,所以我们返回 184 。
示例2:
输入: n = 2
输出: 22
解释: 一些可行的序列为 (1, 2) ,(2, 1) ,(3, 2) 。
一些不可行的序列为 (3, 6) ,(2, 4) ,因为最大公约数不为 1 。
总共有 22 个不同的可行序列,所以我们返回 22 。
4.2 思路
动态规划,动态数组为dp[i][j][k],意为第i颗骰子的点数为j、上一颗骰子点数为k的方案数,那么dp[i][j][k]可以由上一次投掷结果转移而来,即当当前的j和k以及l满足两两互不相等均不相同且相邻之间的最大公约数为1,那么则有dp[i][j][k] += dp[i-1][k][l].
首先通过gcd()求出点数之间的最大公约数:
/*辗转相除法*/
int gcd(int a, int b) {
if(b == 0) return a;
return gcd(b, a%b);
} 最外层遍历骰子编号,第二层遍历当前骰子点数,第三层遍历前一个骰子点数,第四层遍历上上个骰子的点数;由于需要用到前两次的结果,因而初始化dp[3],而后最外层的遍历从4开始,因此,需要将n<=2作为特殊情况处理。
class Solution {
int gcd(int a, int b) {
if(!b) return a;
return gcd(b, a % b);
}
int mod = 1e9 + 7;
public:
int distinctSequences(int n) {
static int dp[10001][7][7], G[7][7];
memset(dp, 0, sizeof(dp));
if(n == 1) return 6;
else if(n == 2) return 22;
for(int i = 1; i < 7; ++i) for(int j = 1; j < 7; ++j)
G[i][j] = gcd(i, j);
for(int i = 1; i < 7; ++i) for(int j = 1; j < 7; ++j) for(int k = 1; k < 7; ++k)
if(i!=j && i!=k && j!=k && G[i][j]==1 && G[j][k]==1)
++dp[3][i][j];
for(int i = 4; i <= n; ++i) for(int j = 1; j < 7; ++j) for(int k = 1; k < 7; ++k)
if(k != j && gcd(j, k) == 1) for(int l = 1; l < 7; ++l)
if(l != j && gcd(k, l) == 1)
dp[i][j][k] = (dp[i][j][k] + dp[i-1][k][l]) % mod;
int ans = 0;
for(int i = 1; i < 7; ++i) for(int j = 1; j < 7; ++j)
ans = (ans + dp[n][i][j]) % mod;
return ans;
}
};
