leetcode-weekly-contest-299

Cpp 动态规划 力扣周赛
刷题
发布日期:   2022-06-26

Problem List

1. 判断矩阵是否是一个 X 矩阵

1.1 题目描述

如果一个正方形矩阵满足下述 全部 条件，则称之为一个 X 矩阵 ：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0
给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例1：

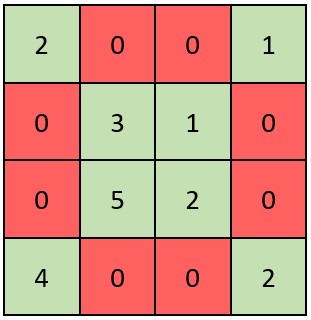
输入： grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出： true
解释： 矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例2：

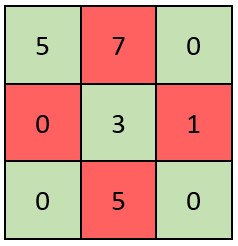
输入： grid = [[5,7,0],[0,3,1],[0,5,0]]
输出： false
解释：
矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

1.2 思路

  直接模拟即可。

  • 当当前遍历的元素不为0则判断当前位置是否为主对角线上的元素，是则继续遍历，否则返回false. 主对角元素具有两个性质：①横索引等于纵索引；②横索引加纵索引等于n-1；
  • 当当前遍历的元素为0则判断当前位置是否为主对角线上的元素，是则返回false，否则继续遍历。
  • 如果完成遍历则说明该矩阵为X矩阵，返回true.
class Solution {
public:
    bool checkXMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        for(int r = 0; r < n; ++r){
            for(int c = 0;  c < n; ++c){
                if(grid[r][c] == 0){
                    if(r == c || r+c == n-1)    return false;
                }else{
                    if(!(r == c || r+c == n-1)) return false;
                }
            }
        }
        return true;
    }
};

2. 统计放置房子的方式数

2.1 题目描述

一条街道上共有 n * 2 个 地块 ，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 109 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例1：

输入： n = 1
输出： 4
解释： 可能的放置方式：

  1. 所有地块都不放置房子。
  2. 一所房子放在街道的某一侧。
  3. 一所房子放在街道的另一侧。
  4. 放置两所房子，街道两侧各放置一所。

示例2：

输入： num = 37, k = 2
输出： -1
解释： 个位数字为 2 的整数无法相加得到 37 。

示例3：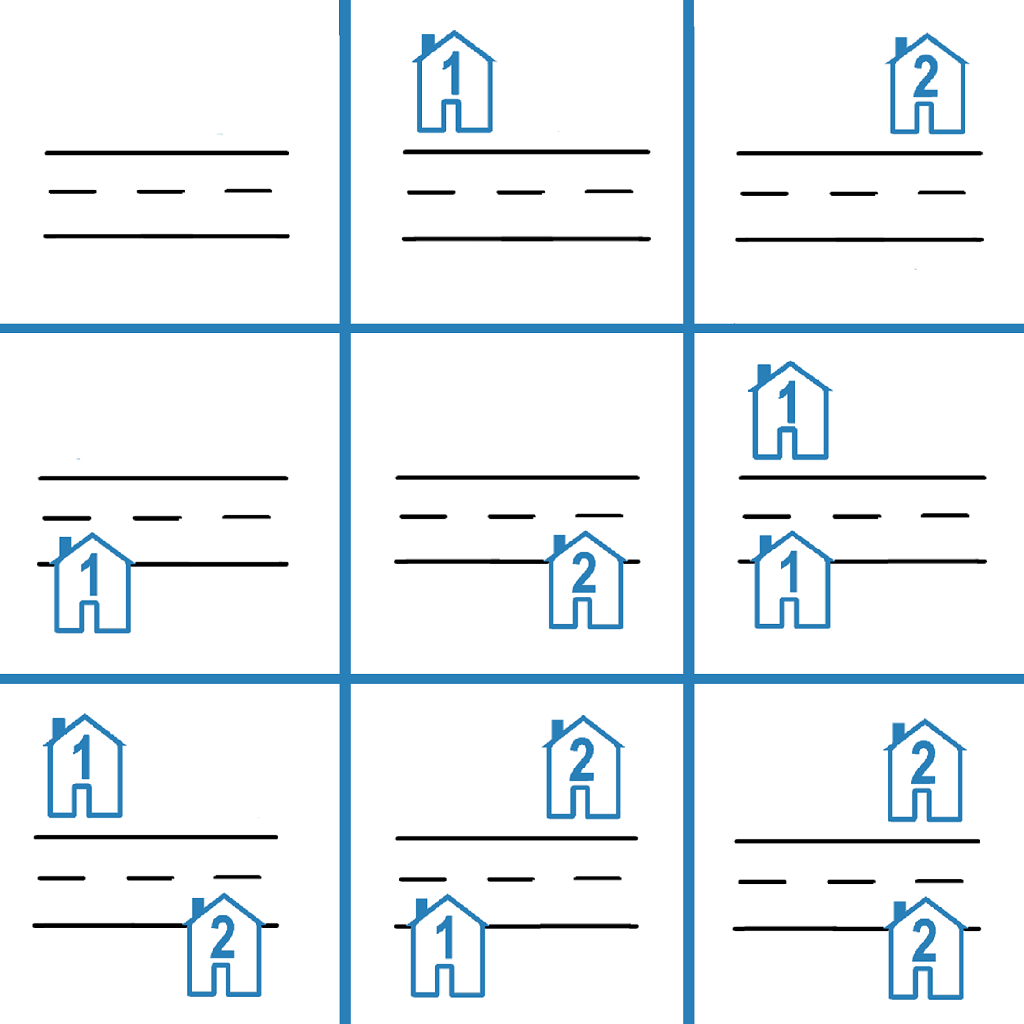

输入： n = 2
输出： 9
解释： 如上图所示，共有 9 种可能的放置方式。

2.2 思路

  动态规划。求”街道”两侧放置房屋的方式数目，实际上就可以看作求单侧的房屋方式数组，然后平方就是答案。

  动态规划数组意义：每一块空地都有两种状态：放置房屋与空闲两种。则可以设动态数组为dp[n+1][2]，其中第一个索引代表有多少个空地，第二个索引代表状态，为1则该空地上有房子，为0则没有。进一步的，dp[i][1]代表前i块地块在第i块地块上有房子的情况下的房屋放置方式数目，dp[i][0]代表前i块地块在第i块地块上没有房子的情况下的房屋放置方式数目。

  dp[i][0]无所谓第i-1有房子还是没房子，所以是由dp[i-1][0]和dp[i-1][1]转移而来；而dp[i][1]必定由dp[i-1][0]转换而来，因为相邻的位置上不能同时有房子。

class Solution {
    int mod = 1e9 + 7;
public:
    int countHousePlacements(int n) {
        vector<vector<long long>> dp(n+1, vector<long long> (2, 1));
        for(int i = 1; i <= n; ++i){
            dp[i][0] = (dp[i-1][0] + dp[i-1][1]) % mod;
            dp[i][1] = dp[i-1][0];
        }
        return 1ll*dp[n][0]*dp[n][0]%mod;
    }
};

注意这里不能用max(dp[n][0], dp[n][1]),因为前边求动态规划数组的时候进行了求余操作，如果不进行求余，那么max之后结果是dp[n][0]，而求余之后max就可能变成dp[n][1]了，导致错误。

  上述代码中可以进行简化，dp[i][0]由上个位置的两种状态转移而来，而dp[i][1]只是由上个位置没房子这种状态转移来的。由dp[i][0]=dp[i-1][0]+dp[i-1][1]和dp[i][1] = dp[i-1][0]可以得到dp[i+1][0]=dp[i][0]+dp[i][1]=dp[i][0]+dp[i-1][0],也就变成了dp[i][0]=dp[i-2][0] + dp[i-1][0],所以就变成了斐波那契数列了。

class Solution {
    int mod = 1e9 + 7;
public:
    int countHousePlacements(int n) {
        vector<long long> dp(n+1);
        dp[0] = 1, dp[1] = 2;
        for(int i = 2; i <= n; ++i){
            dp[i] = (dp[i-2] + dp[i-1]) % mod;
        }
        return 1ll*dp[n]*dp[n]%mod;
    }
};

3. 拼接数组的最大分数

3.1 题目描述

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度都是 n 。

你可以选择两个整数 left 和 right ，其中 0 <= left <= right < n ，接着 交换 两个子数组 nums1[left...right] 和 nums2[left...right]。

例如，设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ，整数选择 left = 1和 right = 2，那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。
你可以选择执行上述操作 一次 或不执行任何操作。

数组的 分数 取 sum(nums1) 和 sum(nums2) 中的最大值，其中 sum(arr) 是数组 arr 中所有元素之和。

返回 可能的最大分数 。

子数组 是数组中连续的一个元素序列。arr[left...right] 表示子数组包含 nums 中下标 left 和 right 之间的元素（含 下标 left 和 right 对应元素）。

示例1：

输入： nums1 = [60,60,60], nums2 = [10,90,10]
输出： 210
解释： 选择 left = 1 和 right = 1 ，得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。

示例2：

输入： nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出： 210
解释： 选择 left = 3 和 right = 4 ，得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。

示例3：

输入： nums1 = [7,11,13], nums2 = [1,1,1]
输出： 31
解释： 选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。

3.2 思路

  有点类似于滑动窗口。先求两个数组的前缀和，分别为sum1和sum2,然后遍历sum1，并在sum2中找一段连续子序列的和大于sum1的对应的子序列，并将二者的差值和sum1[n]的加和更新到答案中；然后再遍历sum2，一样的道理，找sum1中的加和大于sum2中对应位置的加和的连续子序列并更新答案。这里对两个数组分别进行遍历，其实就是将大的交换到sum1求最大值，然后将大的交换到sum2中求最大值。

class Solution {
public:
    int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size();
        vector<int> sum1(n+1, 0), sum2(n+1, 0);
        for(int i = 1; i <= n; ++i){
            sum1[i] = sum1[i-1] + nums1[i-1];
            sum2[i] = sum2[i-1] + nums2[i-1];
        }
        int ans = sum2[n];
        for(int l = 0, r = 1; r <= n; ++r){
            if(sum1[r]-sum1[l] > sum2[r]-sum2[l]){
                ans = max(ans, sum2[n] + sum1[r]-sum1[l] - (sum2[r]-sum2[l]));
                continue;
            }
            l = r;
        }
        ans = max(ans, sum1[n]);
        for(int l = 0, r = 1; r <= n; ++r){
            if(sum2[r]-sum2[l] > sum1[r]-sum1[l]){
                ans = max(ans, sum1[n] + sum2[r]-sum2[l] - (sum1[r]-sum1[l]));
                continue;
            }
            l = r;
        }
        return ans;
    }
};

注意这里窗口左端点的更新，应该是l = r而不是l++,因为更新左端点时意味着sum1（或sum2）中的l~r-1这一段加和是大于另一个数组的，而l~r则已经小于另一个数组，那么就直接将左端点更新到右端点位置.切记不能更新到下个位置r+1,因为前缀和数组是滞后于原数组一个位置的。

  • 别人的写法:
class Solution {
    int d[100048], n;
public:
    int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
        n= int(nums1.size());
        int sum1 = 0, sum2 = 0;
        for (int i = 0; i < n; i++)
        {
            d[i] = nums2[i] - nums1[i]; // 求两个数组每一项的差
            sum1 += nums1[i];           // 前缀和
            sum2 += nums2[i];           // 前缀和
        }
        
        // 找出nums2中比nums1大最多的那一段连续子数组，这里用贪心求
        int maxn = 0, cur = 0;
        for (int i = 0; i < n; i++)
        {
            cur += d[i];                // 累加数组差
            maxn = max(maxn, cur);     
            if (cur < 0) cur = 0;
        }
        int ans = sum1 + maxn;          // 将差最大的那一段换到nums1中      
        
        // 找出nums1中比nums2大最多的那一段连续子数组
        // 由于d是num2-num1，那么这里的d就是求最小值，且为负
        int minn = 0; cur = 0;
        for (int i = 0; i < n; i++)    
        {
            cur += d[i];
            minn = min(minn, cur);
            if (cur > 0) cur = 0;
        }
        ans = max(ans, sum2 - minn);    // 更新答案
        return ans;
    }
};
  • 另一位大佬的写法：
class Solution {
    int s1[100005],s2[100005],s[100005];
public:
    int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size(),i,m1,m2,ans;
        for(i=0;i<n;i++)
        {
            s1[i+1]=s1[i]+nums1[i]; // 前缀和
            s2[i+1]=s2[i]+nums2[i];
            s[i+1]=s1[i]-s2[i];     // 差的前缀和
        }
        ans=max(s1[n],s2[n]);       // 可能不交换的时候已经是最大的
        for(i=m1=m2=0;i<=n;i++)
        {
            m1=max(m1,s[i]);
            m2=min(m2,s[i]);
            ans=max(ans,max(max(s1[n]-s[i]+m1,s2[n]+s[i]-m1),max(s1[n]-s[i]+m2,s2[n]+s[i]-m2)));
        }
        return ans;
    }
};

思路大同小异，都是分成两步来算，有可能是将nums1中一部分换到nums2得到最大，也可能是nums2中一部分换到nums1来得到最大。

文章作者: Vyron Su
文章链接: http://example.com/2022/06/26/leetcode-weekly-contest-299/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Vyron Su !
Cpp 动态规划 力扣周赛