leetcode-biweekly-contest-82

刷题

发布日期: 2022-07-10

Problem List

[1] 计算布尔二叉树的值
[2] 坐上公交的最晚时间
[3] 最小差值平方和

1. 计算布尔二叉树的值

1.1 题目描述

给你一棵 完整二叉树 的根，这棵树有以下特征：

叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。
非叶子节点要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。
计算一个节点的值方式如下：

如果节点是个叶子节点，那么节点的值为它本身，即 True 或者 False 。
否则，计算两个孩子的节点值，然后将该节点的运算符对两个孩子值进行运算。
返回根节点 root 的布尔运算值。

完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。

叶子节点 是没有孩子的节点。

示例1：

输入： root = [2,1,3,null,null,0,1]
输出： true
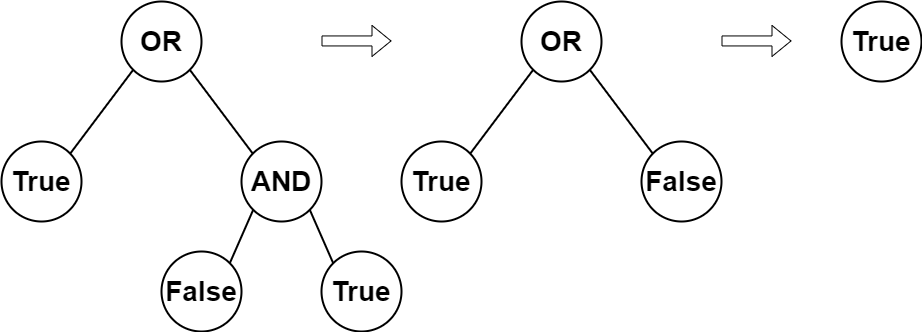
解释： 上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ，所以我们返回 true 。

示例2：
输入： root = [0]
输出： false
解释： 根节点是叶子节点，且值为 false，所以我们返回 false 。

1.2 思路

简单递归遍历一下树并检查当前节点是否为叶节点，若是则返回当前节点的值(0对应false, 1对应true)，如果不是则按当前节点值继续往下递归，为2则左右子树的值进行或操作，为3则进行与操作。树为完整二叉树，不存在只有单个节点的非叶节点。

class Solution {
public:
    bool evaluateTree(TreeNode* root) {
        if(!root->left && !root->right) return root->val;
        if(root->val == 2) {
            return evaluateTree(root->left) || evaluateTree(root->right);
        }
        return evaluateTree(root->left) && evaluateTree(root->right);
    }
};

2. 坐上公交的最晚时间

2.1 题目描述

给你一个下标从 0 开始长度为 n 的整数数组 buses ，其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ，其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同，所有乘客到达的时间也互不相同。

给你一个整数 capacity ，表示每辆公交车最多能容纳的乘客数目。

每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达，公交在 x 时刻出发，满足 y <= x 且公交没有满，那么你可以搭乘这一辆公交。最早到达的乘客优先上车。

返回你可以搭乘公交车的最晚到达公交站时间。你不能跟别的乘客同时刻到达。

注意：数组 buses和 passengers 不一定是有序的。

示例1：

输入： buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出： 16
解释： 第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达，所以你必须在第二位乘客之前到达。

示例2：

输入： buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
输出： 20
解释： 第 1 辆公交车载着第 4 位乘客。
第 2 辆公交车载着第 6 位和第 2 位乘客。
第 3 辆公交车载着第 1 位乘客和你。

2.2 思路

很直接的思路，遍历到最后一辆车的最后一名上车的乘客，然后往前遍历找插入的位置。

实现步骤：

~~用一个set按顺序存放乘客到达的时间~~（无需此操作）；
对buses和passengers数组分别进行按升序顺序排序；
遍历公车：对每一辆车，当当前遍历到的乘客到达的时间小于等于公车到站时间，即passengers[index] <= buses[i]时，且公车上还有座位，该乘客可以上当前遍历的公车，用一个变量res来记录当前公车的最后一个上车的人；
遍历完成后res其实就是最后一辆车的最后一个上车的乘客，那么我们只需要比这个乘客到达的时间早即可(满座的情况下)，即循环自减1直至set中没有出现res，此时res即为答案。

如果最后一辆车没满座，说明可以最后一辆车的时间点上车即可，即返回最后一辆车的到站时间buses[n-1]（n为公车的数量）；
如果最后一辆车满座，则向前遍历，直至当前的时间点没有乘客到达，返回这个时间点即可。

更新：并不需要set来判断当前时间点是否有乘客同时到达，我们通过index可以知道最后一个上车的人的时间点，我们必须要比这个最后一个上车的人的时间早，那么res就是必须小于passengers[index-1],index指向的是最后一个上车的人的后继元素，那么当passengers[index-1]==res说明当前时刻有乘客一起到达，要早一点，因而--res并判断上个人是否在这个时间点到达。更新后的代码如下(更新前没必要的操作已经注释掉了)。

class Solution {
public:
    int latestTimeCatchTheBus(vector<int>& buses, vector<int>& passengers, int capacity) {
        //set<int> s;
        //for(int i: passengers)  s.insert(i);
        sort(buses.begin(), buses.end());
        sort(passengers.begin(), passengers.end());
        int index = 0, res, n = passengers.size();
        for(int x: buses) {
            int y = capacity;
            while(y > 0 && index < n && passengers[index] <= x) {
                --y;        
                res = passengers[index++];
            }
            if(y > 0)   res = x;            // 当前公车没满座，则最后一个应该等于公车到达的时间
        }
        while(index>0 && passengers[--index]==res)  --res;  // 贪心求解
        //while(s.count(res)) --res;
        return res;
    }
};

3. 最小差值平方和

3.1 题目描述

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度为 n 。

数组 nums1 和 nums2 的 差值平方和 定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])2 之和。

同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的，你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。

请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小 差值平方和 。

注意：你可以将数组中的元素变成负整数。

示例1：

输入： nums1 = [1,2,3,4], nums2 = [2,10,20,19], k1 = 0, k2 = 0
输出： 579
解释： nums1 和 nums2 中的元素不能修改，因为 k1 = 0 和 k2 = 0 。
差值平方和为：(1 - 2)2 + (2 - 10)2 + (3 - 20)2 + (4 - 19)2 = 579.

示例2：

输入： nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
输出： 43
解释： 一种得到最小差值平方和的方式为：

将 nums1[0] 增加一次。

将 nums2[2] 增加一次。
最小差值平方和为：
(2 - 5)2 + (4 - 8)2 + (10 - 7)2 + (12 - 9)2 = 43 。
注意，也有其他方式可以得到最小差值平方和，但没有得到比 43 更小答案的方案。

3.2 思路

先求差值(绝对值)数组diff，并求差值数组的加和，如果加和sum <= k1 + k2，则可以将差值数组全部变为0，因而返回0；通过二分法查找大值们最多可以一起减到的值target，即求最小的target值，使得差值数组中所有大于target的项与target的差的加和小于等于k1+k2；求得target后，将diff数组中所有大于这个的值的项变为target，同时将操作次数k1+k2减去对应的次数；如果完成操作后还有剩余的操作数，则将数组中为target的项再减去1直至操作数为0；最后求平方和即可。

class Solution {
    bool check(vector<int> diff, int mid, int cnt) {
        long long sum = 0;
        for(int i: diff) {
            sum += (max(i, mid) - mid);
        }
        return sum <= cnt;
    }
public:
    long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
        int n = nums1.size(), cnt = k1 + k2;
        long long sum = 0;
        vector<int> diff(n);
        for(int i = 0; i < n; ++i) {
            diff[i] = abs(nums1[i] - nums2[i]);
            sum += diff[i];
        }
        if(sum <= cnt)  return 0;
        int target, left = 0, right = 100001;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(check(diff, mid, cnt)) {
                target = mid;
                right = mid - 1;
            }else {
                left = mid + 1;
            }
        }
        for(int i = 0; i < n; ++i) {
            if(diff[i] > target) {
                cnt -= (diff[i] - target);
                diff[i] = target;
            }
        }
        for(int i = 0; i < n && cnt > 0; ++i) {
            if(diff[i] == target) {
                --diff[i];
                --cnt;
            }
        }
        long long ans = 0;
        for(int i: diff)    ans += 1ll * i * i;
        return ans;
    }
};