leetcode-437

437. 路径总和 III

1 题目描述

• 题目链接：437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例1：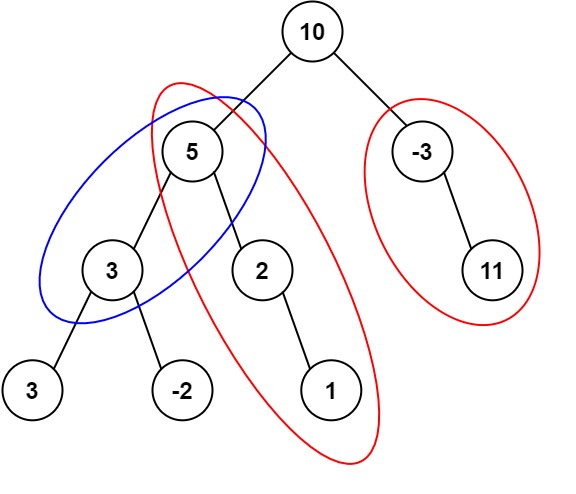

输入: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出: 3
解释: 和等于 8 的路径有 3 条，如图所示。
示例2：
输入: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出: 3

2 思路

• 简单遍历

  题目不要求路径从根节点出发，也不要求终止于叶节点，其实就是以不同的节点为根节点进行深度优先遍历，遍历过程中加入加和是否等于目标和，如果等于则答案加1.

class Solution {
    int ans;
    void dfs(TreeNode* root, int targetSum) {
        if(!root)   return;
        
        dfs1(root, 0, targetSum);       // 以当前节点为根节点向下遍历
        dfs(root->left, targetSum);     // 以当前节点左孩子为根节点
        dfs(root->right, targetSum);    // 以当前节点右孩子为根节点
    }
    void dfs1(TreeNode* root, long long curSum, int targetSum) {
        curSum += root->val;
        if(curSum == targetSum) ++ans;
        if(root->left)  dfs1(root->left, curSum, targetSum);        // 遍历左边路径
        if(root->right) dfs1(root->right, curSum, targetSum);       // 遍历右边路径
    }
public:
    int pathSum(TreeNode* root, int targetSum) {
        ans = 0;
        dfs(root, targetSum);
        return ans;
    }
};

• 哈希前缀和+DFS

  上一种方式实际上会多算很多，比如根节点一直往左走，后边递归会继续在这条路径上遍历(不包含根节点)。采用前缀和的思想，用一个map来存放前缀和，维护根节点到当前节点的前缀和curSum，如果set中出现了curSum - targetSum，则说明自根节点到当前节点中的路径有一些子路径的加和是等于targetSum的，将等于该值的路径数加到答案中。

class Solution {
    int ans;
    void dfs(TreeNode* root, long long curSum, int targetSum, unordered_map<long long, int>& s) {
        if(!root)   return;
        curSum += root->val;
        if(s.count(curSum - targetSum)) ans += s[curSum-targetSum];
        ++s[curSum];
        dfs(root->left, curSum, targetSum, s);
        dfs(root->right, curSum, targetSum, s);
        --s[curSum];
    }
public:
    int pathSum(TreeNode* root, int targetSum) {
        ans = 0;
        unordered_map<long long, int> s;
        s[0] = 1;
        dfs(root, 0, targetSum, s);
        return ans;
    }
};