Topological Sort

拓扑排序是什么？

  对于任何有向图而言，其拓扑排序为其所有结点的一个线性排序（对于同一个有向图而言可能存在多个这样的结点排序）。该排序满足这样的条件——对于图中的任意两个结点u和v，若存在一条有向边从u指向v，则在拓扑排序中u一定出现在v前面。

  对于一个图而言，其拓扑排序存在的条件是该图是一个有向无环图(Directed Acyclic Graph, DAG), 且每个有向无环图至少存在一种拓扑排序。

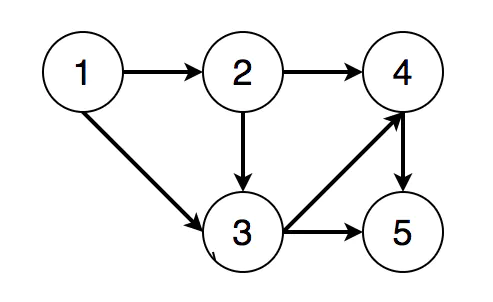
  对于以上的有向图，如果要得到其拓扑排序，那么节点遍历的顺序应该满足：

• 节点1位于节点2、3之前；
• 节点2位于节点3、4之前；
• 节点3位于节点4、5之前；
• 节点4位于节点5之前。

  因而一种有效的拓扑排序就是[1,2,3,4,5].

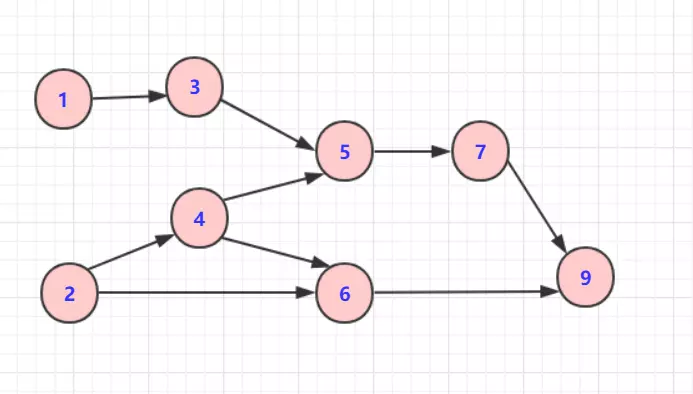
  而对于上边的图，其一种有效的拓扑排序为[1,2,3,4,5,6,7,9]. 这个图有多种拓扑排序，因为前边提到的，有效的拓扑排序只要保证相连节点间的前后顺序即可。

如何实现拓扑排序？

  通常的步骤为：

1. 选择一个入度为0的节点，并将其输出；
2. 删除以该节点为起始的边（以找到下一个入度为0的节点）；
3. 重复以上两个步骤直到所有的顶点都被输出；如果存在顶点没被输出，说明存在环，因而该图不存在拓扑排序。

  具体的实现方法有深度优先搜索和广度优先搜索两种。

• DFS: 通过标记的方法进行图的遍历，当在DFS递归遍历中搜索到已经遍历过的节点，说明图中存在环；否则则将最后一个节点插入栈中，实际上就是先将没有后继节点的节点插入，最后将栈进行输出就是这个图的拓扑排序结果；

• BFS: 首先要求每个节点的入度，然后遍历整个图，将入度为0的节点输出，然后将其后继节点的入度减1，重复以上步骤直至队列中没有节点，此时判断输出的节点数是不是等于总的节点数，若不是说明存在环。

代码实现

class Graph {
    int n;                      // 顶点个数
    vector<vector<int>> edges;  // 邻接表
    queue<int> q;               
    vector<int> indegree;       // 记录节点入度
    vector<int> result;         // 拓扑排序结果
public:
    Graph(int _n) {
        edges.resize(_n);
        indegree = vector<int>(_n, 0);  // 初始化入度为0
    };    
    ~Graph() {};                        // 析构函数
    
    // 向图中添加边
    void addEdge(int u, int v) {
        edges[u].emplace_back(v);
        ++indegree[v];
    }

    // 拓扑排序
    bool topologicalSort(void) {
        for(int i = 0; i < n; ++i) 
            if(indegree[i]==0)  q.emplace(i);
        while(!q.empty()) {
            int cur = q.front();
            q.pop();
            result.emplace_back(cur);       // 输出该顶点
            // 将由cur指向的顶点的入度减1
            for(int next: edges[cur]) 
                if(!(--indegree[next]))     // 入度为0，则入队
                    q.emplace(next);
        }
        if(result.size() < n)   return false;
        return true;
    }
}

  上边代码是常用的BFS拓扑排序模板，下边给出单独的DFS拓扑排序代码：

void dfs(vector<vector<int>>& edges, vector<int>& indegree, vector<int>& res, int u) {
    res.emplace_back(u);
    --indegree[u];
    for(int v: edges[u]) 
        if(!(--indegree[v]))
            dfs(edges, indegree, res, v);
}
vector<int> topologicalSort(vector<vector<int>>& graph, int n) {
    vector<vector<int>> edges;
    vector<int> res, indegree(n, 0);
    for(auto vec: graph) {
        ++indegree[vec[0]];
        edges[vec[1]].emplace_back(vec[0]);
    }
    for(int i = 0; i < n; ++i) 
        if(indegree[i] == 0) 
            dfs(edges, indegree, res, i);
    if(res.size() < n)  return {};
    return res;    
}

力扣相关题目

• 207. 课程表

class Solution {
    int count;
    void dfs(vector<vector<int>>& edges, vector<int>& indegree, int u) {
    ++count;
    --indegree[u];
    for(int v: edges[u]) 
        if(!(--indegree[v]))
            dfs(edges, indegree, v);
    }
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> edges(numCourses);
        vector<int> indegree(numCourses, 0);
        count = 0;
        for(auto vec: prerequisites) {
            ++indegree[vec[0]];
            edges[vec[1]].emplace_back(vec[0]);
        }
        for(int i = 0; i < numCourses; ++i) 
            if(indegree[i] == 0) 
                dfs(edges, indegree, i);
        return count==numCourses;
    }
};

• 210. 课程表 II

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> edge(numCourses);
        vector<int> indgree(numCourses, 0);
        for(auto vec: prerequisites) {
            edge[vec[1]].emplace_back(vec[0]);
            ++indgree[vec[0]];
        }
        vector<int> res;
        for(int i = 0; i < numCourses; ++i)
            if(indgree[i] == 0) res.emplace_back(i);
        int index = 0;
        while(index != res.size()) {
            int cur = res[index++];
            for(int i: edge[cur]) {
                if(!(--indgree[i]))     res.emplace_back(i);
            }
        }
        if(res.size() < numCourses) return {};
        return res;
    }
};

-